Повышение эффективности использования автобусов при выполнении городских пассажирских перевозок в городе Гомель

Параметры (коэффициенты) уравнений определяются по следующим зависимостям:

(2.6)

; (2.7)

, (2.8)

где yэi -экспериментальные значения зависимой переменной в i-х расчетных точках.

Проверка адекватности уравнения многочлена ряда Фурье экспериментальным данным производится по критерию Фишера. При этом при расчете числа степеней свободы под числом факторов понимается число использованных гармоник ряда Фурье.

Мерой согласованности может служить также коэффициент средней линейной ошибки аппроксимации E:

. (2.9)

При проведении расчетов номера гармоник, включаемые в уравнение, рекомендуется принимать адаптивно по максимуму значения статистики критерия Фишера F или минимуму коэффициента средней линейной ошибки аппроксимации E. Гармоники, которые вызывают уменьшение значения F или увеличение значения E, не включаются в модель связи. При этом верхнее значение номера гармоник не должно быть больше чем n/2.

Изучение статистических зависимостей основывается на корреляционно-регрессионном анализе. Корреляционный анализ позволяет ответить на вопрос о существовании зависимости между случайными величинами, а также оценить степень тесноты статистической зависимости. Инструментом регрессионного анализа является уравнение регрессии. Исходными данными для проведения корреляционно-регрессионного анализа является статистическая информация, содержащая значения факторов и зависимого от них параметра.

Одной из возможных схем проведения корреляционно-регрессионного анализа является следующая:

1) проводится взаимный парный корреляционный анализ между всеми возможными сочетаниями факторов и дублирующие факторы исключаются (из дублирующих друг друга факторов для дальнейших расчетов один из них исключают - обычно зависимый);

2) принимается вид уравнения регрессии (модели связи);

3) рассчитываются параметры уравнения регрессии;

4) проверяется значимость отдельных факторов в модели и адекватность уравнения регрессии экспериментальным данным в целом. Если нет малозначимых факторов и уравнение регрессии согласуется с экспериментальными данными - решение получено, а иначе на п.5;

5) отбрасываются малозначимые факторы и проводятся новые расчеты (п. 2-4 или 3,4).

Полученное уравнение регрессии является моделью связи между факторным пространством и зависимым параметром.

Если связь оказалась несущественной, то расчеты или повторяют с другим видом уравнения регрессии или прекращают.

Статистикой, характеризующей тесноту связи между факторами и зависимой переменной, является коэффициент множественной корреляции.

Коэффициент множественной корреляции показывает какая часть дисперсии зависимой переменной объясняется принятой регрессионной моделью:

, (2.10)

где - объясненная сумма квадратов отклонений от оценки математического ожидания (m – число опытов);

- полная сумма квадратов отклонений от оценки математического ожидания;

а0 - оценка математического ожидания случайной величины.

Разность между полной и объясненной суммой квадратов является остаточной (необъясненной) суммой отклонений от оценки математического ожидания

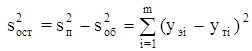. (2.11)

Тогда через значение коэффициента множественной корреляции рассчитывается по формуле:

(2.12)

Значения R может быть в пределах от 0 до 1.0. При R = 0 связь между факторами и зависимой переменной отсутствует, а R = 1.0 указывает на функциональную зависимость.

Для проверки гипотезы существенности коэффициента множественной корреляции и согласованности уравнения регрессии с экспериментами данными используется статистика критерия Фишера:

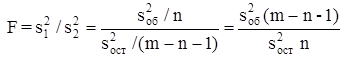(2.13)

или

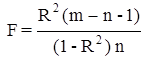, (2.14)

где и - соответственно объясненная и остаточная дисперсия для зависимого параметра.

Чтобы не было оснований отвергнуть гипотезу, что экспериментальные данные согласуются с полученным уравнением регрессии, рассчитанная статистика критерия Фишера должна быть больше табличного значения (F > Fт). Табличное значение Fт определяется в зависимости от уровня значимости и числа степеней свободы k1 = n и k2= m - n- 1 (n – число факторов).

Уровень значимости (вероятность) рекомендуется принимать 0.01 - 0.05 (чем меньше, тем жестче требования к адекватности модели).

Если F < Fт , то считается, что уравнение регрессии не согласуется с экспериментальными данными.

Табличные значения критерия Фишера приведены ниже в таблице 2.1.[12].

Таблица 2.1 - Табличные значения критерия Фишера

 Скачать реферат