Повышение эффективности использования автобусов при выполнении городских пассажирских перевозок в городе Гомель

Статистику критерия Фишера можно использовать для оценки значимости отдельных факторов. Фактор является малозначимым в том случае, если его исключение из модели не вызывает существенного снижения статистики критерия Фишера. При этом исключение малозначимого фактора может обеспечить увеличение статистики F .

2.2 Определение закономерностей изменения пассажиропотоков во времени

Для суще

ствующей маршрутной сети определим значения спроса на перевозку используя многочлен Фурье. Для расчета выберем маршруты №1, 4, 5, 12, 16, и 25, так как на них наиболее значимые пассажиропотоки, что позволит получить более точные характеристики.

Доли пассажиропотоков приходящиеся на каждый месяц года, по сравнению с июнем месяцем, представлены графически на рисунке 2.1.

Рисунок 2.1 – Доли пассажиропотока по месяцам года

Соответственно доли пассажиропотоков по дням недели, по сравнению со средой, представлены графически на рисунке 2.2.

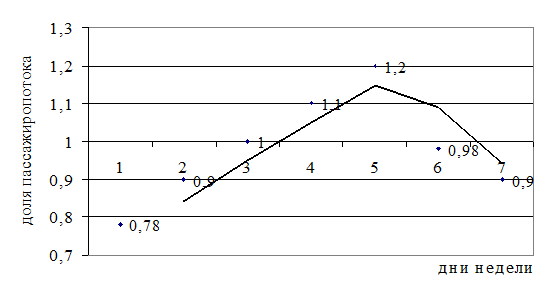
Рисунок 2.2 - Доли пассажиропотоков по дням недели

Приведем пример расчета многочлена Фурье для расчета часовых пассажиропотоков на маршруте №1 «Вокзал – Любенский» в июнь месяц, день недели – среда.

Параметры (коэффициенты) многочлена Фурье рассчитаем по формулам (2.6) – (2.8):

при m=18, k=9:

Параметры многочлена Фурье сведем в таблицу 2.1.

Таблица 2.1 – Параметры многочлена Фурье

Теоретические значения часовых пассажиропотоков рассчитаем по формуле (2.2):

при k=1:

yт1=1003,78+(43,735*cos(2*3,14*1*1/18)+18,418*sin(2*3,14*1*1/18)+

+(-43,735*cos(2*3,14*1*2/18)+ 18,418*sin(2*3,14*1*2/18)+

+(-43,735*cos(2*3,14*1*3/18)+ 18,418*sin(2*3,14*1*3/18)+

+(-43,735*cos(2*3,14*1*4/18)+ 18,418*sin(2*3,14*1*4/18) +

+(-43,735*cos(2*3,14*1*5/18)+ 18,418*sin(2*3,14*1*5/18) +

+(-43,735*cos(2*3,14*1*6/18)+ 18,418*sin(2*3,14*1*6/18) +

+(-43,735*cos(2*3,14*1*7/18)+ 18,418*sin(2*3,14*1*7/18) +

+(-43,735*cos(2*3,14*1*8/18)+ 18,418*sin(2*3,14*1*8/18) +

+(-43,735*cos(2*3,14*1*9/18)+ 18,418*sin(2*3,14*1*9/18);

yт1=969.

Теоретические значения часовых пассажиропотоков рассчитанные и далее для различных гармоник сведем в таблицу 2.2.

Коэффициент средней линейной ошибки аппроксимации E рассчитывается по формуле (2.9):

Е=1/18*(abs((341-339)/339)+ abs((337-1960)/1960)+ abs((801-2006)/2006)+ abs((1101-1362)/1362)+ abs((1087-1200)/1200)+ abs((760-825)/825)+ abs((683-534)/534)+ abs((614-314)/314)+ abs((556-582)/582)+ abs((701-701)/701)+ abs((846-1361)/1361)+ abs((846-2249)/2249)+ abs((1010-1876)/1876)+ abs((915-860)/860)+ abs((728-407)/407)+ abs((615-1003)/1003)+ abs((214-450)/450)+ abs((55-145)/145));

Е=0,559;

Коэффициент множественной корреляции R рассчитывается по формуле (2.10):

Sоб=(339-1003,78)2+(1960-1003,78)2+(2006-1003,78)2+(1362-1003,78)2+(1200-1003,78)2+(825-1003,78)2+(534-1003,78)2+(314-1003,78)2+(582-1003,78)2+(701-1003,78)2+(1361-1003,78)2+(2249-1003,78)2+(1876-1003,78)2+(860-1003,78)2+(407-1003,78)2+(1003-1003,78)2+(450-1003,78)2+(145-1003,78)2;

Sоб=23180,5;

Sп=(341-1003,78)2+(337-1003,78)2+(801-1003,78)2+(1101-1003,78)2+(1087-1003,78)2+(760-1003,78)2+(683-1003,78)2+(614-1003,78)2+(556-1003,78)2+(701-1003,78)2+(846-1003,78)2+(846-1003,78)2+(1010-1003,78)2+(915-1003,78)2+(728-1003,78)2+(615-1003,78)2+(214-1003,78)2+(55-1003,78)2;

Sп=9043657;

R=0,0506;

Статистика критерия Фишера рассчитывается по формуле (2.14):

F=0,00228.

Для остальных гармоник расчеты производятся аналогично.

при k=2:

Е=0,416;

Sоб=5553657;

Sп=9043657;

R=0,784;

F=1,415.

Так как на втором шаге коэффициент средней линейной ошибки аппроксимации E уменьшился, коэффициент множественной корреляции R и критерий Фишера увеличились, то вторая гармоника включается в многочлен Фурье.

при k=3:

Е=0,703;

Sоб=6005277;

Sп=9042657;

R=0,815;

F=1,757.

Так как на третьем шаге коэффициент средней линейной ошибки аппроксимации E увеличился, коэффициент множественной корреляции R и критерий Фишера увеличились, то третья гармоника не включается в многочлен Фурье.

при k=4:

Е=0,295;

Sоб=7061269;

Sп=9043657;

R=0,884;

F=3,167.

Так как на четвертом шаге коэффициент средней линейной ошибки аппроксимации E уменьшился, коэффициент множественной корреляции R и критерий Фишера увеличились, то четвертая гармоника включается в многочлен Фурье.

при k=5:

Е=0,298;

Sоб=7916001;

Sп=9043657;

R=0,936;

F=6,240.

Так как на пятом шаге коэффициент средней линейной ошибки аппроксимации E уменьшился, коэффициент множественной корреляции R и критерий Фишера увеличились, то пятая гармоника включается в многочлен Фурье.

при k=6:

Е=0,347;

Sоб=8093962;

Sп=9043657;

R=0,946;

F=7,576.

Так как на шестом шаге коэффициент средней линейной ошибки аппроксимации E увеличился, коэффициент множественной корреляции R и критерий Фишера увеличились, то шестая гармоника не включается в многочлен Фурье.

 Скачать реферат