Физика разрушения горных пород при бурении нефтяных и газовых скважин

Для нахождения слагаемых Wф и Wv будем использовать следующее очевидное равенство, связывающее главные нормальные напряжения 1, 2, 3 тензора напряжений, среднее нормальное напряжение ср, главные нормальные напряжения тензора-девиатора s1 = (s1  s), s2 = (s2 s>), s3 = (s3 s):

s1 = s1 + s, s2 = s2 + s, s3 = s3 + s

и аналогичные выражения для главных линейных деформаций e1, e2, e3:

e1 = e1 + e, e2 = e2 + e, e3 = e3 + e,

где e1 = e1  e, e2 = e2  e, e3 = e3  e представляют собой главные линейные деформации девиатора деформаций.

Подставляя эти выражения в формулу (5) для W, найдем

2W = (s1e1 + s2e2 + s3e3) + 3se + e(s1 + s2 + s3) + s(e1 + e2 + e3).

В полученном выражении члены (s1 + s2 + s3) и (e1 + e2 + e3) тождественно равны нулю. Это означает, что, учитывая (51), можно записать следующие выражения для энергии формоизменения Wф и энергии изменения объёма рассматриваемого кубика Wv:

Wф = (s1e1 + s2e2 + s3e3) / 2;

Wv = 3se/ 2.

Используя следующие выражения закона Гука для изотропного тела:

s1 = 2Ge1, s2 = 2Ge2, s3 = 2Ge3, ср = 3Kср;

из предыдущих выражений получим

W = (s12 + s22 + s32) / (4G);

Wv = s2 / (2K).

Выражению для Wф можно придать и другой вид

W = I2(T)/(2G) = ti2/(2G),

где I2(Tнд) – второй инвариант девиатора напряжений.

Выражение для энергии упругого деформирования окончательно принимает вид

W = s2/(2K) + ti2/(2G).

2.4 Геометрическая интерпретация напряженного состояния

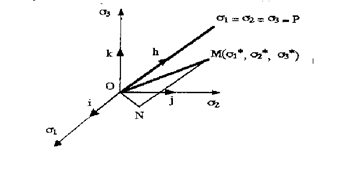
Прежде всего, дадим геометрическую интерпретацию напряженного состояния изотропного тела, отобразив это состояние в трехмерном пространстве главных нормальных напряжений 1, 2, 3 (рис. 4).

Начало координат соответствует отсутствию напряжений в теле. На осях координат лежат точки, отображающие простое растяжение или сжатие вдоль этих осей. На координатных плоскостях 12,23, 13 расположены точки, отображающие плоское напряженное состояние.

Прямая, наклоненная под одинаковыми углами  (cos  = 3-0,5) ко всем трем координатным осям, называется пространственной диагональю или гидростатической осью. Она определяет положение точек, соответствующих гидростатическому состоянию: s1 = s2 = s3 = P.

Рис. 4. Геометрическая интерпретация напряженного состояния

Единичный векторh, направленный вдоль гидростатической оси, определяется выражением

h = (i + j + k),

где i,j, k – единичные вектора по направлению осей 1, 2, 3 (рис. 4). Плоскость, проходящая через начало координат (т.О) и перпендикулярная вектору h, называется девиаторной плоскостью.

Так как направление нормали к девиаторной плоскости задается проекциями вектора h на оси координат, то из общего уравнения плоскости, проходящей через рассматриваемую точку с координатами (1*, 2*, 3*),

A(s1  s1*) + B(s2  s2*) + C(s3  s3*) = 0,

где A= i,B= j,C= k, следует, что уравнение такой плоскости имеет вид

s1 + s2 + s3 = 0.

Любая точка M трехмерного пространства 1, 2, 3, имеющая координаты 1*, 2*, 3*, изображает некоторое напряженное состояние, характеризуемое главными напряжениями 1, 2, 3 (Рис. 4).

Дадим геометрическую интерпретацию величинам ср и i. В качестве образа напряженного состояния мы будем рассматривать не точку М, а вектор ОМ, соединяющий начало координат О с точкой М(1, 2, 3):

 = s1*i + s2* j + s3* k.

Если мы разложим вектор OM, характеризующий напряженное состояние, на составляющие MN и ON, параллельную и перпендикулярную гидростатической оси, соответственно, то составляющая MN определится выражением MN = (OMh)h, где

OMh = (s1*i + s2*j + s3*k)(i + j + k) = (s1* + s2* + s3*)/ =

s×.

Следовательно

MN = s×h = s(i + j + k),

т.е. проекция вектора напряжений OM на гидростатическую ось пропорциональна величине среднего напряжения ср.

Учитывая выражения для векторов MN и OM, можно записать

ON = OM  MN = (s1*i + s2*j + s3*k)  s(i + j + k) =

= (s1  s)i + (s2  s)j + (s3  s) k.

В последнем выражении величины, находящиеся в круглых скобках, представляют собой главные нормальные девиаторные напряжения

s1 = (s1  s), s2 = (s2  s), s3 = (s3  s).

Так как векторONпо определению перпендикулярен гидростатической оси, то он должен лежать в девиаторной плоскости. Иначе говоря, проекции вектора напряженийOM (1*, 2*, 3*) на девиаторную плоскость равна «вектору девиаторных напряжений» s1 , s2 , s3. Иначе это можно выразить и так: точкаN– проекция точки M на девиаторную плоскость – изображает девиаторные напряжения, отвечающие точ-кеM. Любой вектор, принадлежащий девиаторной плоскости, характеризует девиатор напряжений какого-либо напряженного состояния M(1*, 2*, 3*).

Радиальное расстояние между любой точкой, находящейся на гидростатической оси, и точкойM, расположенной на плоскости, параллельной девиаторной плоскости (в частности, расстояние между точкой O (начало координат) и точкой N, расположенной на девиаторной плоскости, проходящей через начало координат), найдем по известной (раздел курса математики «Аналитическая геометрия в пространстве») формуле

 Скачать реферат