Разработка методики обучения интегрального исчисления функции двух переменных

Доказательство. Так как область (P) замкнута, то по теореме Вейерштрасса существуют наибольшее и наименьшее значения функции в области (P).

Пусть М – наибольшее значение функции , m – наименьш

ее значение функции в области (P).

Из теоремы 1 следует, что

Тогда по теореме Больцано-Коши непрерывная функция проходит через все промежуточные значения.

Значит, в области (P) существует точка такая, что .

Поэтому в соответствии с теоремой 1 получаем:

[1].

2.2 Вычисление двойного интеграла

Вычисление двойного интеграла повторным интегрированием в случае прямоугольной области

Сначала рассмотрим двойной интеграл по некоторому прямоугольнику со сторонами, параллельными осям координат [1].

Теорема. Если для функции , определенной в прямоугольнике , существует двойной интеграл

и при каждом постоянном значении из существует определенный интеграл

,

то существует также повторный интеграл

,

и выполняется равенство

.

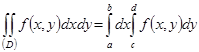Доказательство. Изобразим область (рис. 17).

Разобьем отрезки и соответственно на и частичных отрезков

,

.

Тогда область разобьется на nk частичных прямоугольников.

Частичный прямоугольник определяется так:

.

Пусть

Обозначим через точную нижнюю и точную верхнюю грани функции в частичном прямоугольнике .

Тогда в каждом частичном прямоугольнике будет выполняться неравенство:

.

Выберем произвольно точку .

Проинтегрируем по y на частичном отрезке неравенство

.

Получим: 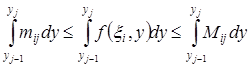, что равносильно

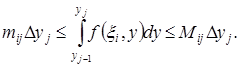
Суммируя последнее неравенство по всем , получим:

.

Так как по условию теоремы существует определенный интеграл

, то (2)

Пусть λ→0 (где λ–наибольший диаметр частичного прямоугольника ), тогда .

Крайние члены двойного неравенства (2) представляют собой верхнюю и нижнюю суммы Дарбу, а значит, они стремятся к двойному интегралу.

Таким образом, должен существовать предел от средней части двойного неравенства и он равен следующему двойному интегралу:

или .

Но по условию теоремы

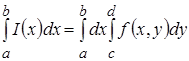[1].

Замечание. Если переменную х поменять на у в рассмотренной теореме, то будет доказано существование повторного интеграла

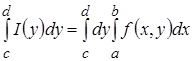
и справедливость формулы [1].

Вычисление двойного интеграла повторным интегрированием в случае криволинейной области

Теорема. Если для функции , определенной в области , ограниченной снизу и сверху двумя непрерывными кривыми:

,

а с боков – двумя ординатами: и , существует двойной интеграл

и при каждом постоянном значении из существует определенный интеграл

,

то существует также повторный интеграл

и выполняется равенство

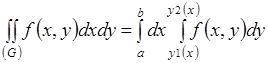[1].

Доказательство. Изобразим область (рис. 18).

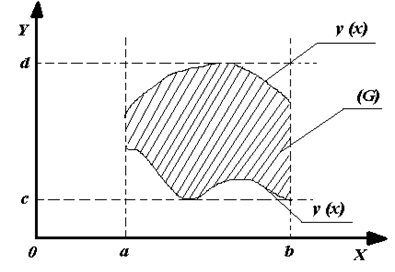
Пусть .

Заключим область в прямоугольник , где