Использование средств ИКТ для повышения степени наглядности при изучении нового материала в курсе геометрии

И Арисмондий с улыбкой взглянул на будущую мать. Та лишь кивнула.

-Тогда не забудь,- обратился жрец к Мнемарху принести богатую жертву храму Аполлона в знак благодарности и смирения перед волей богов. Вот так на земле в древние времена на зелёном острове Самос родился мальчик со странным именем Пифагор

Сообщение 2. Пифагорейский союз и его математические открытия.

О жизни Пифагора и

звестно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.

Родился Пифагор в семье резчика по камню. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.

Пифагор перебрался в город Милет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам когда-то изучал науки.

Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги – в образе полулюдей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем ему было разрешено познакомиться с многовековыми достижениями египетской науки.

Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду.

Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при сёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений.

Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне.

Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.

Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:

теорема о сумме внутренних углов треугольника;

построение правильных многоугольников и деление плоскости на некоторые из них;

геометрические способы решения квадратных уравнений;

деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;

доказательство того, что не является рациональным числом;

создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.

Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания.

После его смерти ученики окружили имя своего учителя множеством легенд.

Подводим итог, кто же такой Пифагор? (Учёный, мыслитель, поборник нравственности, поклонник ЗОЖ). Какие из его нравственных законов вы бы взяли на вооружение и почему?

Повторение и выявление проблемы.

Что нам известно о прямоугольных треугольниках? ( по модели)

1. Определение прямоугольного треугольника.

2. Названия сторон, соотношения между ними.

3. Свойство острых углов прямоугольного треугольника.

4.Свойство прямоугольного треугольника с углом в 30°

5. Свойство прямоугольного треугольника с углом в 45°.

Устно по готовым чертежам (слайд 8) найти неизвестные элементы треугольников.

нам удалось найти?

Проблема - имеющихся знаний недостаточно, чтоб найти в треугольнике АВС катет АС, в треугольнике МРН гипотенузу НР, нужно установить связь между катетами и гипотенузой.

2.3 Формулировка теоремы Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Запишите теорему Пифагора для данных треугольников, найдите катет АС и гипотенузу НР (АС = 6, НР = 5).

2.4. Доказательство теоремы (слайд 13)

( учебник «Геометрия 7-9» Л.С. Атанасяна стр.130)

2.5 Решение задач № 483 (б,г) – фронтально

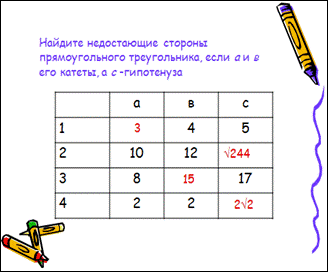
Самостоятельно: Найдите недостающие элементы прямоугольного треугольника, если а и в его катеты, а с – гипотенуза

Проверка (слайд 14)

Дополнительная задача (из «Арифметики» Магницкого)

Случися некоему человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обрете лестницу долготою 125 стоп. И ведати хощет, колико стоп сея лестницы нижний конец от стены отстояти имать.(проверка – слайд 15)

III. Заключительное слово учителя.

Теорема Пифагора издавна широко применялась в различных областях науки, техники и практической жизни. О ней писали в своих произведениях римский архитектор и инженер Ветрувий, греческий писатель – моралист Плутарх, математик 5 века Прокл и другие. Долгое время считалось, что до Пифагора эта теорема не была известна. В настоящее время установлено, что эта теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора.

Мы с вами познакомились с одним из более чем ста пятидесяти геометрических способов доказательства теоремы. Существует легенда о том, что в честь своего открытия Пифагор принёс в жертву 100 быков.

Пребудет вечной истина, как скоро

Ее познает слабый человек!