Использование законов и свойств арифметических действий при формировании вычислительных навыков

1) 4 + (2+1) = 4 + 3 = 7;

4+2+ 1 = 6+1 =7;

4 + (2+1) = 5 + 2 = 7.

Проанализируем эти способы. В случае 1 вычисления выполнены в соответствии с указанным порядком действий. В случае 2 применено сочетательное свойство сложения. Вычисления же в последнем случае опираются па переместительный и сочетательный законы сложения, причем промежуточные преобразования опущены. Они таковы. Сначал

а на основании переместительного закона переставили местами слагаемые 1 и 2: 4+(2-1) = 4 + (1+2). Затем воспользовались сочетательным законом: 4 + (1 +2) =(4+ 1) + 2. И, наконец, произвели вычисления согласно порядку действий (4 +1)+ 2 = 5 + 2 = 7.

Правила вычитания числа из суммы и суммы из числа

Обоснуем известные правила вычитания числа из суммы и суммы из числа.

Правило вычитания числа из суммы. Чтобы вычесть число из суммы, достаточно вычесть это число из одного из слагаемых суммы и к полученному результату прибавить другое слагаемое.

Запишем это правило, используя символы: Если а, Ь, с — целые неотрицательные числа, то:

а) при а>с имеем, что (а+Ь) — с = (а — с)+Ь;

б) при Ь>с имеем, что (a+b) — c==a + (b — с);

в) при а>с и Ь>с можно использовать любую из данных формул.

Пусть а >с, тогда разность а —с существует. Обозначим ее через р: а — с =р. Отсюда а = р+с. Подставим сумму р+-с вместо а в выражение (а+Ь) — с и преобразуем его: (а + 6) —с = (р + c+b) — c = p+b+-c — c = p+b

Но буквой р обозначена разность а —с, значит, имеем (а+Ь) — — с = (а — с)+Ь, что и требовалось доказать.

Аналогично проводятся рассуждения и для других случаев. Приведем теперь иллюстрацию данного правила (случай «а») при помощи кругов Эйлера. Возьмем три конечных множества А, В и С, такие, что п(А) = а, п(В) = Ь, п(С) = с и AUB=0, СUА. Тогда {a+b) — с есть число элементов множества (AUB)\C, а число (а — с)+Ь есть число элементов множества {А\С)UВ. На кругах Эйлера множество (АUВ)\С изображается заштрихованной областью, представленной на рисунке .

Легко убедиться в том, что множество (А\С)UВ изобразится точно такой же областью. Значит, (AUB)\C = (A\C)UB для данных

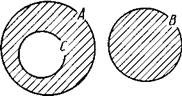
множеств А, В и С. Следовательно, п((АUВ)\С) = п((А\С)UВ)и (а + Ь)— с — (а — с)+Ь.

Аналогично можно проиллюстрировать и случай «б».

Правило вычитания из числа суммы. Чтобы вычесть из числа сумму чисел, достаточно вычесть из этого числа последовательно каждое слагаемое одно за другим, т. е. если а, Ъ, с — целые неотрицательные числа, то при а>Ь+с имеем а—(Ь+с) = (а — Ь)—с.

Обоснование этого правила и его теоретико-множественная иллюстрация выполняются так же, как и для правила вычитания числа из суммы.

Приведенные правила рассматриваются в начальной школе на конкретных примерах, для обоснования привлекаются наглядные изображения. Эти правила позволяют рационально выполнять вычисления. Например, правило вычитания из числа суммы лежит в основе приема вычитания числа по частям:

5-2 = 5-(1 + 1) = (5-1)-1=4-1=3.

Смысл приведенных правил хорошо раскрывается при решении арифметических задач различными способами. Например, задача «Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок. 6 лодок вернулись. Сколько лодок с рыбаками должно еще вернуться?» может быть решена тремя способами:

/ способ. 1. 20 + 8 = 28 2. 28 — 6 = 22

// способ. 1. 20 — 6=14 2. 14 + 8 = 22

III способ. 1. 8 — 6 = 2 2. 20 + 2 = 22

Законы умножения

Докажем законы умножения, исходя из определения произведения через декартово произведение множеств.

1.Переместительный закон: для любых целых неотрицательных чисел а и Ъ справедливо равенство a•b = b•a.

Пусть а = п(А), Ь = п(В). Тогда по определению произведения а•Ь = п{А•В). Но множества А•В н В•А равномощны: каждой паре (а, Ь) из множества АХВ можно поставить в соответствие единственную пару (Ь, а) из множества ВхА, и наоборот. Значит, п(АХВ) = п(ВхА), и поэтому a-b = n {AXB) = n (BXA) = b-а.

2. Сочетательный закон: для любых целых неотрица тельных чисел а, Ь, с справедливо равенство (а• Ь) •с = а• (Ь•с).

Пусть а = п(А), b = п (В), с = п (С). Тогда по определению произведения {a-b)-c = n((AXB)XQ, a a-(b -c) = n (AX(BXQ). Множества (АхВ)ХС и А X {ВХ Q различны: первое состоит из пар вида ((а, Ь), с), а второе — из пар вида (а, (Ь, с)), где а£А, Ь£В, с£С. Но множества (АХВ)ХС и АХ(ВХС) равномощны, так как существует взаимно однозначное отображение одного множества на другое. Поэтому п{(АХВ) •С) = п {А•(В•С)), и, значит, (а•Ь) •с = а• (Ь•с).

3. Распределительный закон умножения относительно сложения: для любых целых неотрицательных чисел а, Ь, с справедливо равенство (a +b) x c = ac+ be.

Пусть а — п (А), Ь = п (В), с = п(С)и АUВ= 0. Тогда по определению произведения имеем (a+b) x c = n ((AUB) • C. Откуда на основании равенства (*) получаем п ((А UВ) • С) = п((А • С)U(В• С)), и далее по определению суммы и произведения п ((А • С)U(В• С)) — = п(А•С) + п(В•С) = ас + Ьс.

4. Распределительный закон умножения относительно вычитания: для любых целых неотрицательных чисел a, b и с и a^b справедливо равенство (а — Ь)с = = ас — Ьс.

Этот закон выводится из равенства (А\В) •С = (А •С)\(В•С) и доказывается аналогично предыдущему.

Переместительный и сочетательный законы умножения можно распространить на любое число множителей. Как и при сложении, эти законы часто используются совместно, т. е. произведение нескольких множителей не изменится, если их переставить любым способом и если любую их группу заключить в скобки.

Распределительные законы устанавливают связь умножения со сложением и вычитанием. На основе этих законов происходит раскрытие скобок в выражениях типа (а+Ь)с и (а — Ь) с, а также вынесение множителя за скобки, если выражение имеет вид ас —be или

ас + Ьс.

В начальном курсе математики изучается переместительное свойство умножения, оно формулируется так: «От перестановки множителей произведение не изменится» — и широко используется при составлении таблицы умножения однозначных чисел. Сочетательный закон в начальной школе в явном виде не рассматривается, но используется вместе с переместительный при умножении числа на произведение. Происходит это следующим образом: учащимся предлагается рассмотреть различные способы нахождения значения выражения 3• (5•2) и сравнить полученные результаты.

Приводятся случаи:

1) 3• (5•2) = 3•10 = 30;

2) 3• (5•2) = (3•5) •2 = 15•2 = 30;

3) 3• (5•2) = (3•2) •5 = 6•5 = 30.

Первый из них основан на правиле порядка действий, второй — на сочетательном законе умножения, третий — на переместительном и сочетательном законах умножения.

Распределительный закон умножения относительно сложения рассматривается в школе на конкретных примерах и носит название правил умножения числа на сумму и суммы на число. Рассмотрение этих двух правил диктуется методическими соображениями.

Правила деления суммы на число и числа на произведение

Познакомимся с некоторыми свойствами деления натуральных чисел. Выбор этих правил определен содержанием начального курса математики.