Элементы наглядной топологии в профильной школе

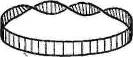
Задача 13. Докажите, что трижды перекрученная лента (рисунок) гомеоморфна ленте Мёбиуса, а ее край изотопен простому узлу.

Домашнее задание.

Задачи: 2, 5, 6, 11, 13.

Методика проведения занятия по теме «двумерные поверхности»

Тема: Двумерные поверхности.

Тип урока: Урок введения нового материала,

урок-практикум.

Цели урока:

Обучающая: Обеспечить формирование целостной системы ведущих знаний о предмете топология.

Ознакомить с понятием двумерных поверхностей.

Развивающая: Обеспечить у школьников развитие пространственного мышления.

Оборудование:

Литература;

Доска.

Приложения (иллюстрации) у каждого ученика.

Этапы урока:

Организационный момент.

Проверка домашнего задания.

Актуализация знаний.

Введение нового материала.

Закрепление изученного материала:

- Решение задач практического содержания.

Итог урока:

- Подведение итогов урока;

- Подведение итогов элективного курса.

Ход урока.

Двумерные поверхности.

Сегодня на уроке мы познакомимся с понятием двумерных поверхностей, а также рассмотрим их виды. Для начала разберемся, что же такое поверхность?

Определение 1. Фигура, у которой каждая точка х имеет окрестность, гомеоморфную кругу (внутри которого лежит точка х), называется двумерной поверхностью. Примером таких поверхностей является сфера (рис.1) и тор (рис.2).

Рисунок 1

Рисунок 2

Рассматривают также поверхности с краем. Круг – поверхность с краем. Сфера, в которой вырезаны несколько круглых отверстий (рис.3), также является поверхностью с краем.

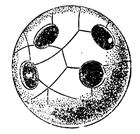
Рисунок 3

Рассмотрим другие примеры двумерных поверхностей на наглядных примерах: следующие поверхности можно получить, склеивая противоположные стороны прямоугольника. Склеиваемые стороны обозначаются одинаковыми буквами и стрелками в зависимости от направления склеивания.

Лента Мёбиуса.

Интересный пример двумерной поверхности с краем был описан в 1862—1865 годах в работах немецких математиков Мёбиуса и Листинга. Она получается следующим образом: прямоугольник один раз перекручивается, и затем ее концы склеиваются (рис.4). Полученная поверхность с краем называется лентой Мёбиуса:

Рисунок 4

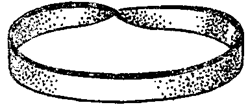
Рисунок 5

Эта поверхность имеет лишь одну сторону. Посмотрите, пожалуйста, на иллюстрацию 1 (см. Приложение II). Например, перемещая кисточку по листу Мёбиуса

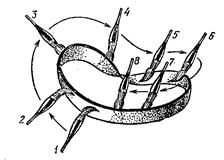
мы придем к тому же месту, с которого начинали закрашивание, но с обратной стороны. Перемещая кисточку дальше, мы закрасим весь лист Мёбиуса и убедимся, что у него нет «второй стороны».

Лента Мёбиуса обладает любопытными свойствами. Если попробовать разрезать ленту вдоль по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двухсторонняя (вдвое больше закрученная, чем лента Мёбиуса) лента, которую фокусники называют «афганская лента». Если теперь эту ленту разрезать вдоль посередине, получаются две ленты намотанные друг на друга. Если же разрезать ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна — более тонкая лента Мёбиуса, другая — длинная лента с двумя полуоборотами (Афганская лента). Другие интересные комбинации лент могут быть получены из лент Мёбиуса с двумя или более полуоборотами в них. Например, если разрезать ленту с тремя полуоборотами, то получится лента, завитая в узел трилистника.

Лист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — лист Мёбиуса, показывает муравьёв, ползающих по поверхности ленты Мёбиуса (иллюстрация 1).

Существуют технические применения ленты Мёбиуса. Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему работать дольше, потому что вся поверхность ленты изнашивается равномерно. Также в системах записи на непрерывную плёнку применяются ленты Мёбиуса (чтобы удвоить время записи). Во многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.