Решение треугольников в 9 классе

в) b < a, то решение единственное – угол b может быть только острым, так как против большей стороны лежит больший угол, то a b.

Необходимо сделать заметку, что эту задачу можно решить иным способом. С помощью теоремы косинусов найти наибольший угол, воспользовавшись теоремой синусов, найти любой другой угол (он заведомо буд

ет острым); третий угол находится из равенства a + b + g = 180°. Данный случай рекомендуется дать сильным ученикам в качестве домашнего задания.

Если в условии задачи на решение треугольников требуется найти угол, то вполне достаточно определить одну из его тригонометрических функций, так как умение пользоваться таблицами и микрокалькулятором для нахождения тригонометрических функций угла и наоборот, нахождение угла по заданной одной из его тригонометрических функций, не является программным. Если учитель сочтет нужным, то можно объяснить учащимся, как пользоваться таблицами и микрокалькулятором. Но есть значения тригонометрических функций, которые учащиеся должны знать – это углы 30°, 45°, 60°, 90°, 135° и 150°. И предлагается следующие виды уроков.

Урок 1:Синус, косинус, тангенс. Основное тригонометрическое тождество

Цели урока:

образовательная: повторить определение синуса, косинуса и тангенса острого угла прямоугольного треугольника; ввести понятия синуса, косинуса и тангенса для углов от 0° до 180° и закрепить их знание в ходе решения задач;

развивающая: развить логическое мышление, быстроту внимания; формировать приемы умственной деятельности: сравнения, аналогии, сопоставления, углублять и систематизировать знания по данной теме; формировать умения видеть ключевую задачу в более сложной математической задаче; развивать точную, лаконическую речь;

воспитательная: учить преодолевать трудности; работать в быстром темпе, собираться мыслями и принимать решение; воспитывать стремление к совершенствованию знаний.

Ход урока

I. Организационный момент (2мин).

Учитель приветствует учеников, проверяет присутствующих, знакомит учащихся с темой целями урока.

II. Повторение ранее изученного материала (5 мин).

Учитель: Ребята, что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника?

Ученик 1: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Ученик 2: Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Ученик 3: Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Учитель: Какое равенство мы называем основным тригонометрическим тождеством?

Ученик: Равенство вида sin2A+cos2A=1 – называют основным тригонометрическим тождеством.

Учитель: Чему равно значение синуса, косинуса и тангенса для угла 30°

Ученик: .

Учитель: Чему равно значение синуса, косинуса и тангенса для угла 45°

Ученик: .

Учитель: Чему равно значение синуса, косинуса и тангенса для угла 60°

Ученик: .

III. Изучение нового материала (15 мин).

Учитель: Ребята, введем понятие единичной полуокружности. Как нам это сделать?

Ученик 1: Сначала, нам надо ввести прямоугольную систему координат Oxy. Построим полуокружность радиуса 1, с центром в начале координат, расположенную в первом и втором квадрантах, её мы и назовем единичной полуокружностью.

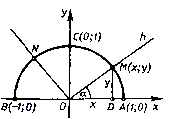
Учитель: Да, это верно. А теперь, давайте рассмотрим понятие синуса и косинуса для углов 0° < а < 180°?

Ученик: Для этого нам надо, из точки О мы проведем луч h, пересекающий единичную полуокружность в точке М (х; у). Обозначим буквой a угол между лучом h и положительной полуосью абсцисс.

Учитель: А что делать, если луч совпал с положительной полуосью абсцисс?

Ученик: Если луч h совпадает с положительной полуосью абсцисс, то будем считать, что a = 0°.

Учитель: А если угол a - острый?

Ученик: Если угол a острый, то из прямоугольного треугольника DOM имеем:

.

Но по рисунку мы видим, что ОМ=1, MD=y, OD=x, поэтому sina=y, cosa=x. (1)

Учитель: Что мы можем сказать о синусе, косинусе острого угла a.

Ученик: Синус острого угла a равен ординате у точки М, а косинус угла a— абсциссе х точки М.

Учитель: Давайте, рассмотрим случай, когда угол a - тупой, развернутый или прямой?

Ученик: Если угол a прямой, тупой или развернутый (углы АО С, AON и АО В на рисунке) или a=0°, то синус и косинус угла a также определим по формулам (1).

Учитель: Итак, подведем итог всему выше сказанному. Что называется синусом угла a? А косинусом угла a?

Ученик 1: Для любого угла a из промежутка 0°180°, синусом угла a называется ордината у точки М.

Ученик 2: Косинусом угла a, из промежутка 0°180°, называется абсцисса х точки М.

Учитель: А что, мы можем сказать о значении синуса и косинуса угла a?

Ученик: Так как координаты (х;у) точек единичной полуокружности заключены в промежутках 01, -11 то для любого a из промежутка 0°180°, справедливы неравенства:

01, -11.

Учитель: Как нам найти значение синуса и косинуса для углов 0°, 90° и 180°.

Ученик 1: Для этого рассмотрим лучи ОА, ОС и ОВ, соответствующие этим углам (см. рис.).

Ученик 2: Нам надо найти координаты точек А, С и В. Они имеют координаты А (1; 0), С (0; 1), В(-1; 0), тогда sin0° = 0, sin 90° = 1, sin 180° = 0, cos 0° = 1, cos 90° =0, cos 180°= -1. (2)

Учитель: Мы нашли синус и косинус. А как нам найти тангенс?

Ученик: Тангенсом угла a называется отношение , то есть

. (3)

Учитель: При всех ли возможных углах будет существовать тангенс угла a?

Ученик: При a = 90° tg a не определен, поскольку cos 90° = 0 и в формуле знаменатель обращается в нуль.

Учитель: Найдите значение тангенса для углов 0° и 180°?

Ученик: Используя формулы (2),мы можем найти значение tg 0° = 0, tg 180°=0.

Учитель: Ребята, давайте вывести основное тригонометрическое тождество, используя рисунок. Что нам для этого надо?