Совершенствование структуры и содержания домашнего задания как формы организации самостоятельной работы учащихся

Ключ к разгадыванию криптограмм содержит ответы на математические вопросы, поэтому расшифровка - полезное занятие. В результате кропотливой работы постепенно складывается мудрое изречение, которое очень интересно домысливать, пока оно еще не полностью составлено, чтобы затем проверить свою догадку, прочитав фразу до конца.

Математические загадки (головоломки) - некоторые рассчитаны на приме

нение обычных правил сложения, вычитания, умножения и деления, а для иных понадобиться более абстрактные математические понятия, операции и размышления. Это магические квадраты, волшебные сечения, мозаичные головоломки, задачи на топологии и другие. Головоломки различаются по сложности, но все они математически строги к тому же требуют нестандартного подхода.

Творческий характер носят задания моделирование различных макетов. Например, при изучении в 6 классе темы "Координаты на прямой", учащимся предлагается дома изготовить модель координатной прямой, которая будет активно использоваться на протяжении изучения всей темы "Положительные и отрицательные числа". Также при изучении темы "Прямоугольный параллелепипед" домашним заданием может служить изготовление макета параллелепипеда, успевающие учащиеся должны сами изготовить его развертку, а слабым учащимся она может быть предоставлена учителем. В старших классах учащиеся выполняют макеты более сложных объемных фигур.

Домашним заданием творческого характера также может служить изготовление наглядных методических пособий, плакатов имеющих методическую ценность.

Например, к обобщающему уроку по теме "Тригонометрические уравнения" учащимся предлагается классифицировать все известные методы решения тригонометрических уравнений и оформить это в виде плаката или еще каким-либо образом.

И нельзя упомянуть о том, что творчество учащегося, несомненно, проявляется и при решении математических задач - главное чтобы эта задача была нестандартной.

Для формирования самостоятельности мышления, воспитания творческой активности необходимо включать нестандартные задачи в систему домашних упражнений.

Нестандартные задачи - это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Однако любая задача, считающаяся стандартной, в тот момент, когда ученик с ней сталкивается впервые, является для него нестандартной. После того, как нестандартная задача решена, любая аналогичная задача становится стандартной.

Таким образом, нестандартная задача ─ это задача, алгоритм решения которой учащимся неизвестен, т.е. учащиеся не знают заранее ни способов её решения, ни того, на какой учебный материал опирается решение.

Как учитель может помочь учащимся решать нестандартные задачи? Универсального метода, позволяющего решить любую нестандартную задачу, нет, т.к. нестандартные задачи в какой-то степени неповторимы.

Рассмотрим отдельные методические приемы обучения учащихся решать нестандартные задачи:

1. Прежде всего, надо отметить, что научить учащихся решать задачи (в т. ч. нестандартные) можно только в том случае, если у учащихся будет желание их решать, т.е. если задачи будут содержательными и интересными с точки зрения ученика. Поэтому задача учителя - вызвать у учащихся интерес к решению той или иной задачи. Необходимо тщательно отбирать интересные задачи и делать их привлекательными для учащихся. Это могут быть - задачи-шутки, задачи-сказки, старинные задачи и т.п. Одно бесспорно: наибольший интерес у школьников вызывают задачи, взятые из окружающей жизни, задачи, связанные со знакомыми вещами, опытом. Важно показать детям, что от решения математической задачи можно получить такое же удовольствие, как от разгаданного кроссворда или ребуса.

2. Задачи не должны быть слишком легкими, но и не слишком трудными, т.к. ученики, не решив задачу или не разобравшись в решении, предложенном учителем, могут потерять веру в свои силы. В этом случае очень важно соблюсти меру помощи. Прежде всего, учитель не должен знакомить учащихся с уже готовым решением. Подсказка должна быть минимальной.

Рассмотрим примеры решения нестандартных задач.

Задание №1.

Прохожий заметил идущий на остановку автобус в 180 метрах позади себя. Чтобы не опоздать, он побежал и через 12 секунд прибежал на остановку одновременно с автобусом. С какой скоростью пришлось бежать прохожему, если известно, что автобус движется со скоростью 19 м/сек?

Прежде чем давать эту задачу на дом, целесообразно прочитать ее в классе и сделать к ней рисунок, т.е. составить графическую модель ситуации, описанной в задаче:

I способ.

1) 19 × 12 = 228 (м) - расстояние, которое проехал автобус;

2) 228 - 180 = 48 (м) - расстояние, которое пробежал прохожий;

3) 48: 12 = 4 (м/с) - скорость прохожего.

Ответ: 4 м/с.

II способ.

1) 180: 12 =15 (м/с) - скорость, с которой автобус догоняет прохожего;

2) 19 - 15 = 4 (м/с) - скорость прохожего.

Ответ: 4 м/с.

Наводящие вопросы, которые могут быть заданы классу:

На какую из ранее решенных задач похожа эта задача?

I способ.

1) Какую величину требуется найти в задаче? (скорость)

2) Какие величины надо знать, чтобы определить скорость движения? (путь и время)

3) Какие из них нам известны? (время)

4) Подумайте, как определить путь.

II способ.

1) О каком движении речь идет в задаче: навстречу, вдогонку, объекты сближаются или удаляются? Как бы вы охарактеризовали скорость, с которой меняется взаимное расположение объектов? (движение вдогонку, автобус догоняет пешехода, скорость сближения)

2) В этой задаче двигаются автобус и прохожий, причем автобус догоняет прохожего. Какие скорости и расстояния рассматриваются, когда речь идет о движении вдогонку? (скорости движущихся объектов, скорость сближения или удаления, расстояние между объектами, время, которое требуется, чтобы одному из них догнать другого).

4) Какие из этих величин известны, какие нет? Какая из них искомая? (известно время, которое потребовалось автобусу, чтобы догнать прохожего, скорость автобуса; неизвестна скорость сближения; искомая величина - скорость прохожего).

5) Как определить неизвестные величины?

Здесь второе решение короче, но додуматься до него труднее. Поэтому не следует торопиться с тем, чтобы дать детям готовое решение, эффект будет минимальный. Лучше к этой задаче возвращаться в течение нескольких уроков, давая детям возможность все глубже осознавать описанную в ней ситуацию.

отрезка ML, 1 длины отрезка MK, 1 длины отрезка NL.

Задание №2.

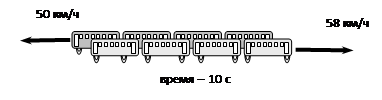
Пассажир поезда, идущего со скоростью 50 км/ч, заметил, что встречный поезд шел мимо него в течение 10 секунд. Определите длину встречного поезда, если его скорость - 58 км/ч.