Теория управления. Принципы системного анализа

3) математические модели. Модели, обладающие абсолютной точностью. К.Маркс и И.Кант говорили о том, что любая отрасль знания может тем с большим основанием называется наукой, чем в большей степени в ней используется математика. Однако, чтобы зайти до использования математической модели в какой-либо области необходимо получить достаточное для этого количество знаний. Отсутствие развитого математ

ического аппарата в какой-либо науке само по себе не означает ее «научности», а есть следствие сложности, недостаточной познанности ее предмета, т.е. временное явление.

Материальные модели

Материальная модель есть реальное, вещественное отображение объекта. Чтобы математическая модель выполняла свою функцию, т.е. замещала в каком-то отношении оригинал, она должна иметь определенное подобие по отношению к оригиналу.

Существуют различные виды подобия.

Прямое подобие – подобие, устанавливаемое в результате физического взаимодействия или последовательности взаимодействий (фотографии, модели самолетов и т.п., макеты зданий, куклы, протезы, шаблоны и т.п.). Однако никакая прямая модель не может быть абсолютной копией оригинала. Существуют проблемы переноса результатов моделирования результатов модельных экспериментов на оригинал (натурный образец). Яркий пример – гидродинамика. Отсюда возникла разветвленная, содержательная теория подобия.

Косвенное подобие. Косвенное подобие не устанавливается человеком, а объективно существует в природе, обнаруживается в виде совпадения или достаточной близости абстрактных моделей и в дальнейшем используется при моделировании.

Например, электромеханическая аналогия (одинаковые уравнения для электрических и механических процессов), шаг как аналог времени, подопытные животные – аналог человеческого организма и т.п.).

Условно подобные модели: подобие этих моделей оригиналу устанавливается в результате соглашения. Пример: деньги (модель стоимости), удостоверение личности (модель владельца), карты (модели местности), сигналы (модели сообщений и т.д.).

Условные подобные модели являются способом материального воплощения абстрактных моделей, вещественной формой, в которой абстрактные модели передаются от одного человека к другому, храниться долгое время, т.е. отчуждаются от сознания, сохраняя, тем не менее, способность возвращения в абстрактную форму. Это достигается с помощью соглашения о том, какое состояние реального объекта ставится в соответствие данному элементу абстрактной модели.

8.5 Место математического моделирования в системных исследованиях

Из рассмотренного ранее нам должно быть понятно, что системный анализ не есть какой-то конкретный метод. Это стратегия научного поиска, которая использует математические концепции, математический аппарат в рамках систематизированного научного подхода к решению сложных проблем. При этом так или иначе выделяется ряд последовательных, взаимосвязанных этапов (рис. 1). Рассмотрение вместо самой системы (т.е. явления, процесса, объекта) и модели всегда связано с упрощением. Главная проблема здесь – выделение тех особенностей, которые существенны для целей рассмотрения. К настоящему времени разработано множество удачных моделей, например, такие как:

конечноэлементная модель для решения различных прикладных задач (статика, динамика, прочность конструкций, динамика оболочек и т.п.);

генетический код;

и др.

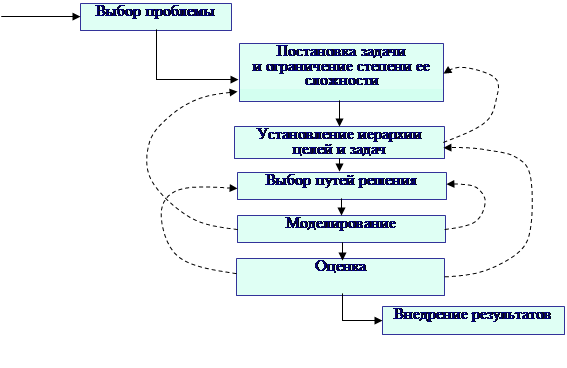
Рис. 4. Решение проблемы

Ранее нами было выделено два основных вида моделей: материальные (макеты, физические модели, масштабированные модели и т.п.) и идеальные (вербальные, знаковые).

При построении моделей процессов в техносфере приходится прибегать как к так называемым интуитивным («ненаучным») моделям, так и к семантическим (смысловым).

Под интуитивным моделированием подразумевают моделирование, использующее представление объекта, не обоснованное с точки зрения формальной логики. Это представление может не поддаваться, или трудно поддаваться формализации или же вообще не нуждаться в ней. Такое моделирование человек осуществляет в своем сознании в форме мысленных экспериментов, сценариев и игровых ситуаций с целью подготовки к предстоящим практическим действиям. Основой для подобных моделей служит опыт – знания и умения людей, а также любое эмпирическое знание, полученное из эксперимента или процесса наблюдения без объяснения причин и механизма наблюдаемого явления.

Семантическое моделирование, в отличие от интуитивного, логически обосновано с помощью некоторого числа исходных предположений. Сами эти предположения нередко облекаются в форму гипотез. Семантическое моделирование предполагает знание внутренних механизмов явления. К методам семантического моделирования относятся вербальное (словесное) и графическое моделирование (рис. 5).

Рис. 5. Виды идеальных моделей

Семиотическое, или знаковое моделирование является, в отличие от семантического, наиболее формализованным, поскольку использует не только слова естественного языка и изображения, но и различные символы – буквы, цифры, иероглифы, нотные знаки. В последующем все они объединяются с помощью специфических правил. К этому виду моделирования относится математическое моделирование.

К знаковым моделям относятся химические и ядерные формулы, графики, схемы, графы, чертежи, топографические карты и т.п. Среди знаковых моделей выделяется их высший класс – математические модели, т.е. модели, при описании которых используется язык математики.

Математическая модель (ММ) – это описание протекания процесса, описание состояния или изменения состояния системы на языке алгоритмических действий с математическими формулами и логических переходов.

Кроме того, ММ допускает работы с таблицами, графиками, номограммами, выбор из совокупности процедур и элементов (последнее подразумевает использование операций предпочтения, частичной упорядоченности, включения, определение принадлежности и т.п.).

Различные математические правила манипулирования со связями системы позволяют делать предсказания относительно тех изменений, которые могут произойти в исследуемых системах, когда изменяются их составляющие.

Сложность формирования математической модели связана с необходимостью владения математическими методами и предметных знаний, т.е. знаний в той области, для которой создается модель. В реальности специалисту в данной практической области часто не хватает математических знаний, сведений о моделировании вообще, а для сложных задач – знания системного анализа. С другой стороны, прикладному математику трудно хорошо ориентироваться в предметной области.

Следует заметить, что деление моделей на вербальные, натурно знаковые в определенной степени условно. Так, существуют смешанные типы моделей, скажем, использующие и вербальные, и знаковые построения. Можно даже утверждать, что нет знаковой модели без сопровождающей описательной – ведь любые знаки и символы необходимо пояснять словами. Часто и отнесение модели к какому-либо типу является нетривиальным.

 Скачать реферат