Методика проведения факультативного курса "Методы решения нестандартных задач по алгебре"

Пример 3. Решить уравнение .

Решение. Заметим, что, Рассмотрим функцию, ее область определения ≠, где ∈ ℤ . Положим, , тогда исходное уравнение запишется в виде . Ясно, что функция нечетная и периодическая с периодом .

Поскольку ′()=( ) ′=> 0, то функция возрастающая на интервале () . Отсюда следует, что уравнение равносильно бесконечной совокупности уравнений , где - произвольное целое число. Выясним, какие из чисел ( решений совокупности) являются решениями исходного уравнения.

Пусть , тогда если =, то. Отсюда .

Пусть , тогда если =, то. Отсюда ,что невозможно.

Следовательно, решениями исходного уравнения являются , где -произвольное целое число, неравное при целом .

Упражнения для самостоятельной работы дома даны в Приложении.

Занятие 10. Разбор наиболее трудных задач для самостоятельной работы и проверочная работа по материалу занятий 7,8 и 9.

Цели: повторить в ходе решения некоторых задач из домашнего задания изученный материал; проверить усвоение применения метода обращения к монотонности функции и метода решения уравнений вида .

В начале занятия предлагается разобрать задачи 4,6 из домашнего задания и несколько задач на темы занятий 7 и 8( на усмотрение учителя). Во второй половине занятия дать проверочную работу. (Решения задач и варианты проверочной работы даны в Приложении).

Занятие 11. Решение уравнения вида и его модификаций

Цели: рассмотреть способы решения уравнений вида , , ; подготовка к зачету.

В начале занятия рекомендуется провести анализ проверочной работы предыдущего занятия.

1. Класс уравнений вида удобен для отработки нестандартных приемов решений. Уравнения такого вида давно присутствуют среди олимпиадных задач. Они интересны тем, что при решении некоторых уравнений данного класса можно воспользоваться свойством непрерывности функции . При решении уравнений указанного вида используется следующее утверждение.

Теорема 1: Если - монотонно возрастающая функция, то уравнения (1) и (2) эквивалентны.

Доказательство То, что уравнение (1) является следствием уравнения (2), очевидно: любой корень (2) удовлетворяет (1). (Если , то ). Докажем, что любой корень уравнения (1) удовлетворяет уравнению (2). Пусть такое, что . Предположим, что , и для определенности . Тогда , что противоречит предположению . Теорема доказана

Пример 1. Решить уравнение

.

Решение. Т.к. 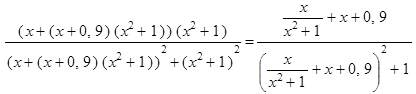, то исходное уравнение принимает вид 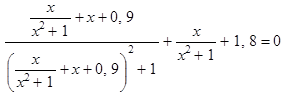. Прибавив к обеим частям уравнения , получим, что уравнение равносильно уравнению вида , причем

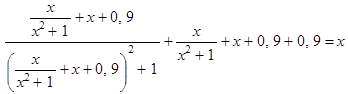
Функция непрерывна на ℝ. По теореме исходное уравнение равносильно уравнению , т.е. уравнению илиили . Это квадратное уравнение не имеет решений (D<0), поэтому и исходное уравнение не имеет действительных корней.