Страница
25

Методика проведения факультативного курса "Методы решения нестандартных задач по алгебре"

2. Обобщением класса уравнений можно считать уравнения вида , где , - некоторые функции. При ≡1 данное уравнение примет вид . Для этого класса уравнений справедливо следующее утверждение.

Теорема 2. Если функция возрастающая и , или функция убывающая и на области допустимых значений уравнения , (3)

то уравнения и равносильны на области допустимых значений уравнения (3).

Пример 2. Решить уравнение .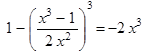

Решение. Область допустимых значений уравнения: ≠0. Положив , замечаем, что уравнение имеет вид .

Т.к. функция убывающая на ℝ (′=) и на области допустимых значений уравнения, то, в силу данной выше теоремы, исходное уравнение равносильно уравнению, т.е. уравнению или . Следовательно, исходное уравнение имеет одно решение .

3. С уравнением тесно связано уравнение вида (4)

где , - некоторые функции и - функция, обратная к функции . Т.к. (⁻¹()) ≡ , то решения уравнений (4) являются корнями уравнения .

Пример 3. Решить уравнение .

Решение. Область допустимых значений уравнения есть ℝ.

Перепишем уравнение в виде: (5) и положим . Отсюда легко заметить, что .

Следовательно, в правой части уравнения (5) стоит функция, обратная к функции и, значит, уравнение (5) имеет вид . Поскольку функция возрастающая, то уравнение (5) равносильно уравнению и, значит, уравнению , т.е. уравнению . Т.к. , то исходное уравнение имеет три корня .

4. В заключение изучения уравнений, составленных из функций, являющихся суперпозициями более простых функций, остановимся на уравнениях вида

, (6)

, (7)

где - некоторая функция, - функция, обратная к функции и левая часть уравнений (6) и (7) есть результат действия раз на (- кратная суперпозиция ). Для уравнения (6) справедлива теорема для уравнения . Примеры решения уравнений вида (6) встречаются часто. Ясно, что решение уравнений (7) сводится к решению уравнений вида (6) [48].

Пример 4. Решить уравнение , где возведение в куб

в левой части уравнения повторяется раз.

Решение. Нетрудно заметить, что уравнение имеет вид (…(())…) = ⁻¹(), причем (если , то ). Поскольку функция возрастающая, то уравнение равносильно уравнению и, следовательно, эквивалентно уравнению, т.е. уравнению , т.е. уравнению , т.е. . Легко заметить, что корень этого уравнения, тогда , причем . Отсюда следует, что исходное уравнение имеет одно решение .