Методика проведения факультативного курса "Методы решения нестандартных задач по алгебре"

Таким образом, показано, что системы (А) и (Б) равносильны в случае, если известно, что хотя бы одна из них имеет решение.

Покажем, что если система (А) не имеет решения, то и система (Б) не имеет решения. Предположим противное, т.е. предположим, что система (Б) имеет решение. Но тогда по доказанному выше и система (А) имеет решение, что противоречит условию, что система (А) не имеет решени

я. Следовательно, наше предположение неверно, а это означает, что система (Б) не имеет решения.

Аналогично можно показать, что если система (Б) не имеет решения, то и система (А) не имеет решения. Следовательно, если не имеет решений хотя бы одна из систем (А) и (Б), то эти системы равносильны. Таким образом, утверждение 3 доказано полностью.

Приведем примеры, использующие утверждение 1.

Пример 1. Решить уравнение (1)

Имеем , .Т.к. функция строго возрастает на ℝ, то на основании утверждения 1 уравнение (1) равносильно уравнению . (2)

Т.к. функция строго убывает на ℝ, то на основании утверждения 1 уравнение (2) равносильно уравнению , (3), имеющему два корня =1 и =2003. Уравнение (1), равносильное уравнению (3), имеет те же два корня. Ответ: 1; 2003.

Пример 2. Решить уравнение (4)

Решение. Имеем , и .Область определения функции есть множество ℝ, функция строго возрастает на ℝ (как сумма строго возрастающих функций). Поэтому на основании утверждения 1 уравнение (4) равносильно уравнению , (5) имеющему две серии решений =,∈ℤ, и =,∈ℤ. Уравнение (4), равносильное уравнению (5) имеет те же решения

Ответ: =,∈ℤ, и =,∈ℤ.

Рассмотрим примеры на применение утверждения 2.

Пример 3. Решить уравнение (6)

Решение. Имеем . Область определения функции это промежуток [-1,1]. На нем функция строго убывает. Поэтому на основании утверждения 2 уравнение (6) равносильна системе

≤1 (7)

Уравнение системы имеет два решения и . Из них двойному неравенству этой системы удовлетворяет только число . Следовательно, система (7) и равносильное ей уравнение (6) имеют то же решение. Ответ: 3.

Разберем пример на применение утверждения 3.

Пример 4. Решить уравнение (8)

Решение. Имеем . Область определения функции есть ℝ, на ℝ функция не является строго монотонной. Однако если заметить, что для любого ∈ℝ ≥0 и ≥0, (9) то получим, что уравнение (8) равносильно системе:

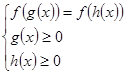(10)

На промежутке J=[0,+ ∞) функция строго убывает. Поэтому по утверждению3 система (10) равносильна системе

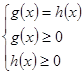(11)

Учитывая условия (9), получаем, что система (11) равносильна уравнению , т.е. уравнению , которое имеет серию решений =,∈ℤ.

Следовательно, исходное уравнение (8) имеет те же решения.

Ответ: =,∈ℤ.

Пример 5.

Решить уравнение (12)

Перепишем уравнение (12) в виде (13)

Т.к. для любого ∈ℝ и , (14)

то, обозначив , получим, что уравнение (13) равносильно системе (15)