Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
при этом
|
|
(2.1.19) |
С учетом (2.1.11) и (2.1.12) полное решение задачи в пространстве изображений представляется как
|
|
(2.1.20) |
|
|
(2.1.21) |
|
|
(2.1.22) |
Для удобства перехода в пространство оригиналов, полученные решения с учётом (2.1.18) представим в форме
|
|
(2.1.23) |
|
|
(2.1.24) |
|
|
(2.1.25) |
Переход в пространство оригиналов осуществим, используя формулы обратного преобразования Лапласа – Карсона [23]:
 ,
,
где ![]() - единичная функция Хевисайда
- единичная функция Хевисайда
|
|
(2.1.26) |
|
|
(2.1.27) |
В нашем случае, совершив обратное преобразование Лапласа – Карсона, и перейдя в пространство оригиналов, решение задачи в нулевом приближении представим в виде
|
|
(2.1.28) |
|
|
(2.1.29) |
|
|
(2.1.30) |
соответственно для пористого, настилающего и подстилающего пластов.
Первый сомножитель в решении (2.1.28) – (2.1.30) описывает уменьшение плотности загрязнителя в результате радиоактивного распада, второй – функция Хевисайда, определяет радиус распространения зоны заражения и третий (выражение в фигурных скобках) учитывает изменение плотности из-за диффузии загрязнителя и радиоактивного распада продиффузирующего нуклида.
Рассмотрим упрощённую модель в которой не учитывается радиоактивный распад в накрывающем и подстилающем пластах. В этом случае в правых частях уравнений (1.5.51), (1.5.53) будет стоять нуль, граничные условия и условия сопряжения не изменятся. Аналогично, в пространстве изображений равны нулю правые части (2.1.1) и (2.1.3). Математическая постановка соответствующей задачи в пространстве изображений
|
|
(2.1.31) |
|
|z| < 1, r >0, |
(2.1.32) |
|
|
(2.1.33) |
|
|
(2.1.34) |
|
|
(2.1.35) |
|
|
(2.1.36) |
|
|
(2.1.37) |
Ход решения идентичен решению задачи с учётом распада в «кровле» и «подошве».
Учитывая граничные условия (2.1.34) и то, что в нулевом приближении плотность загрязнителя в пористом пласте не зависит от z и является функцией только от r и t, решения уравнений (2.2.31), (2.1.33) можно записать в виде
|
|
(2.1.38) |
|
|
(2.1.39) |
Тогда для следов производных, входящих в (2.1.32)
|
|
(2.1.40) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

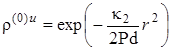 .
.  ,
, 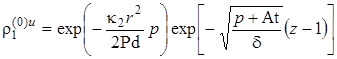 ,
, 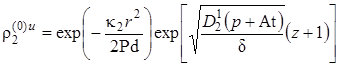 .
.  ,
, 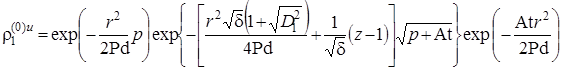 ,
,  .
. 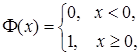
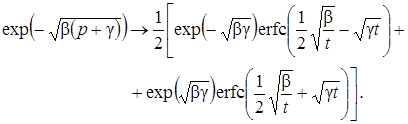

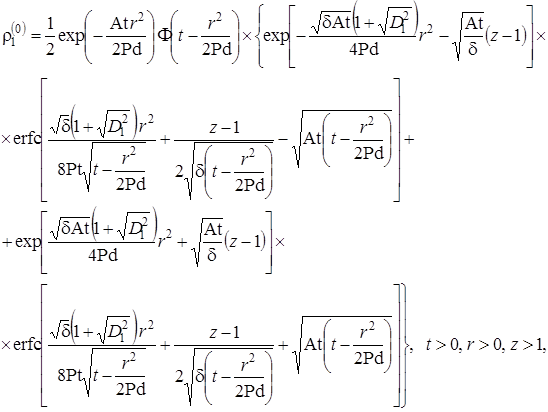

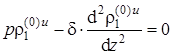 , z > 1, r >0,
, z > 1, r >0,  ,
,
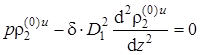 , z < – 1, r >0,
, z < – 1, r >0, 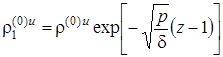 ,
, 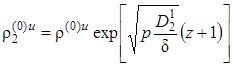 .
. 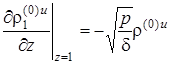 ,
,  .
.