Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты

Усредним задачу по толщине пласта. При усреднении второй производной по вертикальной координате воспользуемся условиями сопряжения (2.6.49)

Окончательно постановка усредн

енной задачи для остаточного члена с учетом (2.6.54) представится как

с граничными условиями и условиями сопряжения

Усредненная задача для остаточного члена (2.6.55) – (2.6.61) имеет тривиальное решение тогда и только тогда, когда

и

то есть, когда в усредненной задаче для остаточного члена отсутствует источник и средние значения нулевого коэффициента разложения на поверхности задания граничных условий обращается в нуль.

В справедливости последнего уравнения легко убедиться, усреднив (2.6.35) с учетом условий сопряжения (2.6.34). Следовательно, если заменить граничное условие для на среднеинтегральное

то рассматриваемый метод решения обеспечивает возможность обращения в нуль решения усреднённой задачи для остаточного члена асимптотического разложения. Это, естественно, повышает ценность решения для практических приложений. В силу этого целесообразно в асимптотических решениях выделить соответствующий класс решений. Асимптотическое приближение параметризованной задачи, полученной из (2.6.4) – (2.6.10), построенное при условии, что решение усредненной задачи для остаточного члена является тривиальным, назовем точным в среднем асимптотическим решением.

Для точного в среднем решения из дополнительного граничного условия (2.6.64) и выражения для первого коэффициента разложения (2.6.22) получим

Откуда

Подставляя полученное таким образом выражение в (2.6.22), для первого коэффициента разложения получим

В первом приближении решение стационарной задачи имеет вид

где и определяются выражениями (2.4.26), (2.4.28) и (2.4.67), (2.4.68)

2.7. Анализ результатов расчёта стационарной задачи

На рис.2.34 представлены графики зависимости стационарного распределения примесей в нулевом приближении от расстояния до оси скважины. Нулевое приближение в данном случае является наиболее значимым, оно определяет общий вид зависимости . При этом величина плотности загрязнителя спадает по экспоненциальному закону и, как следует из графиков, даже для среднеживущих и наиболее опасных радионуклидов (90Sr, 137Cs) на расстояниях 200 h оказывается порядка процентов от максимальной, наблюдающейся в зоне закачки.

На рис 2.35 отражена картина распределения поля радиоактивного загрязнителя в стационарном случае вдоль вертикальной координаты (нулевое приближение). «Срезы» приведены для расстояний 0, 100h и 200h от оси скважины. Видно, что для среднеживущих нуклидов (Т1/2 ~ 30 лет) в настилающем и подстилающем пластах плотности загрязнителя быстро спадают, и уже на расстояниях 0,5h становятся ничтожно малыми.

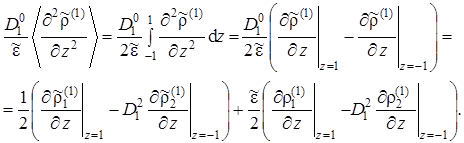
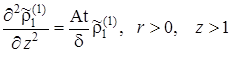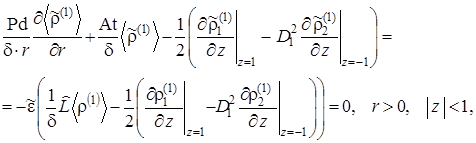
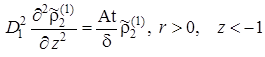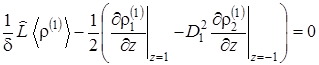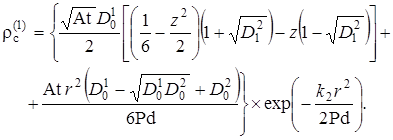
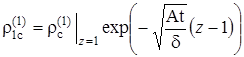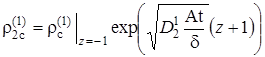 Скачать реферат