Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
1.6. Выводы
В главе I на основе уравнения конвективной диффузии для несжимаемой жидкости с учетом радиоактивного распада и обмена загрязнителя со скелетом, осуществлена постановка термодиффузионной задачи о взаимосвязанных полях концентрации и температуры в глубокозалегающих горизонтах, возникающих при закачке в пористый пласт растворенных радиоактивных веществ. С использованием пара
метра асимптотического разложения температурная и диффузионная задачи представлены в виде бесконечной последовательности краевых задач для коэффициентов разложения искомого решения в асимптотический ряд. Произведено «расцепление» соответствующей цепочки уравнений и на этой основе осуществлена постановка краевых задач смешанного типа со следами производных из внешних областей для нулевого и первого коэффициентов разложения.
При построении решения задачи для первого коэффициента использовано нелокальное граничное условие, заключающееся в том, что средние значения температуры и плотности примесей по толщине пласта на оси скважины равны нулю.
Глава II. РЕШЕНИЕ ЗАДАЧИ МАССОПЕРЕНОСА В НУЛЕВОМ И ПЕРВОМ ПРИБЛИЖЕНИЯХ, СТАЦИОНАРНОЕ РЕШЕНИЕ
2.1. Решение задачи массопереноса в нулевом приближении
В пространстве изображений Лапласа – Карсона
|
|
для нулевого приближения вместо (1.5.51) – (1.5.57) получим следующую задачу:
|
|
(2.1.1) |
|
|z| < 1, r >0, |
(2.1.2) |
|
|
(2.1.3) |
|
|
(2.1.4) |
|
|
(2.1.5) |
|
|
(2.1.6) |
|
|
(2.1.7) |
Решение уравнения (2.1.1) имеет вид
|
|
(2.1.8) |
Учитывая второе из граничных условий (2.1.5), получим ![]() . Тогда
. Тогда
|
|
(2.1.9) |
Аналогично, для подстилающего пласта в пространстве изображений из (2.1.3) и (2.1.5) получим
|
|
(2.1.10) |
Учитывая граничные условия (2.1.4), а также то, что в нулевом приближении плотность загрязнителя в пористом пласте не зависит от z и является функцией только от r и t, эти решения можно переписать в виде
|
|
(2.1.11) |
|
|
(2.1.12) |
Эти выражения позволяют определить значения следов производных из внешних областей, входящих в уравнение для пласта, через плотность примеси в нем
|
|
(2.1.13) |
Подставляя найденные значения производных (2.1.11), (2.1.12) в уравнение (2.1.2), соответствующее (1.5.52) в пространстве изображений, получим
|
|
(2.1.14) |
Группируя слагаемые и учитывая, что в последнем уравнении производная берётся только по одной переменной, перепишем (2.1.2) в виде
|
|
(2.1.15) |
Решение уравнения (2.1.15)
|
|
(2.1.16) |
Граничное условие (2.1.6) позволяет получить значение постоянной интегрирования ![]() . Окончательно в пространстве изображений в нулевом приближении для пористого пласта получим
. Окончательно в пространстве изображений в нулевом приближении для пористого пласта получим
|
|
(2.1.17) |
Введём обозначение для выражения, стоящего в квадратных скобках
|
|
(2.1.18) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

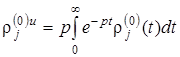 ,
, 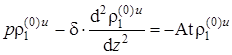 , z > 1, r >0,
, z > 1, r >0,  ,
,
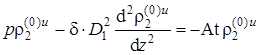 , z < – 1, r >0,
, z < – 1, r >0, 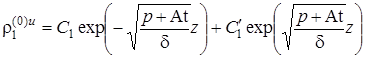 .
. 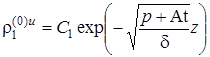 .
. 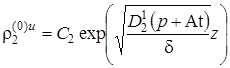 .
. 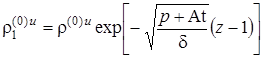 ,
, 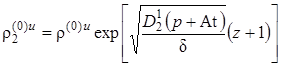 .
. 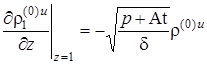 ,
, 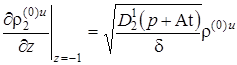 .
. 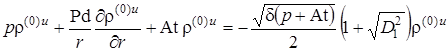 .
. 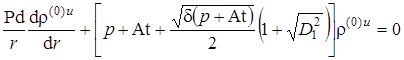 .
. 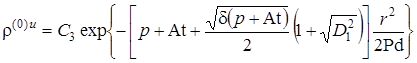 .
. 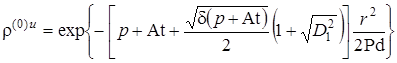 .
. 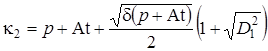 ,
,