Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
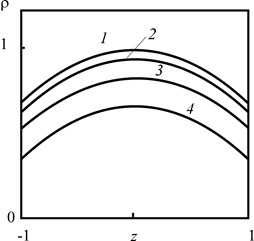
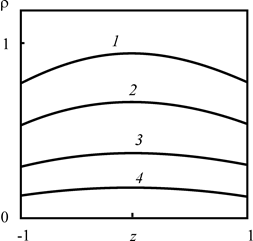
Как видно из рис. 2.30 и 2.31, увеличение времени закачки уменьшает вертикальную составляющую градиента плотности радиоактивного загрязнителя в первом приближении.
|
|
Рис. 2.30. Зави симость |
|
|
Рис. 2.31. Зависимость |
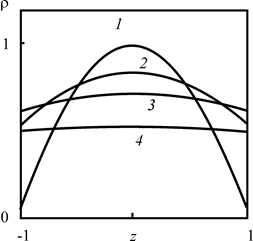
Существенное влияние на распределение загрязнения вдоль вертикальной оси оказывает δ – увеличение коэффициента диффузии несущего пласта (или уменьшение его коэффициента температуропроводности) приводят к более значительному изменению плотности загрязнителя по высоте пласта.
|
|
Рис. 2.32. Зависимость плотности радиоактивных примесей в первом приближении от z для безразмерного времени t = 10 на расстоянии 0.9Rd от оси скважины для различных |
|
|
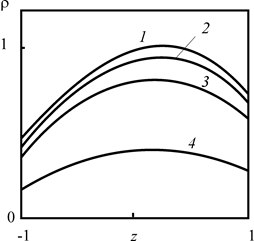
Рис. 2.33. Зависимость |
Различия в физических свойствах «кровли» и «подошвы» приводит к смещению максимума графика ![]() в сторону пласта, обладающего меньшим коэффициентом диффузии.
в сторону пласта, обладающего меньшим коэффициентом диффузии.
Итак, на основе асимптотического метода создана методика расчетов концентрации примесей радиоактивных и химически активных веществ при их захоронении в подземных горизонтах.
2.6. Стационарное решение задачи массопереноса в нулевом и первом приближении
Отметим, что чрезвычайно важным является нахождение стационарного решения, позволяющего установить максимальные размеры зоны загрязнения. Положим в уравнениях (1.5.14) – (1.5.16), описывающих распространение загрязнителя в пластах, первое слагаемое ![]() равным нулю. При этом уравнения принимают вид
равным нулю. При этом уравнения принимают вид
|
|
(2.6.1) |
|
|
(2.6.2) |
|
|
(2.6.3) |
Поделив левые и правые части всех уравнений на ![]() , значение которого определяется выражением (1.5.12), запишем стационарную задачу вместе с граничными условиями и условиями сопряжения
, значение которого определяется выражением (1.5.12), запишем стационарную задачу вместе с граничными условиями и условиями сопряжения
|
|
(2.6.4) |
|
|
(2.6.5) |
|
|
(2.6.6) |
|
|
(2.6.7) |
|
|
(2.6.8) |
|
|
(2.6.9) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

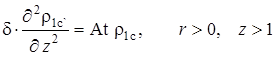 ,
, 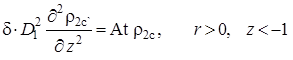 ,
, 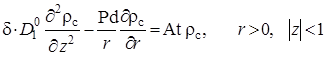 .
. 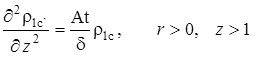 ,
, 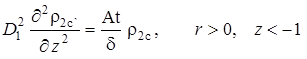 ,
, 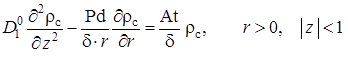 ,
, 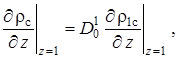
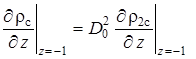 ,
,