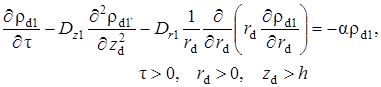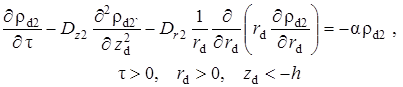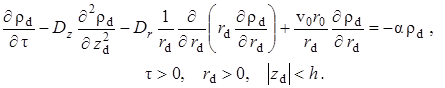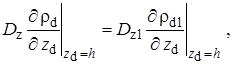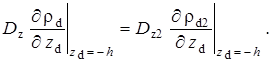Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
Последнее слагаемое в правой части уравнения (1.4.44) устанавливает изменение температуры за счёт энергии, выделяющейся при радиоактивном распаде. Отметим, что температурное поле в нулевом приближении определяется не значениями плотностей радиоактивного загрязнителя в точках, а усреднёнными значениями по вертикальной координате в интервале пласта. Как будет показано ниже, усреднённое таким об
разом значение плотности совпадает с нулевым приближением соответствующей задачи массопереноса (см. пункт 1.5.3).
Для определения в нулевом приближении поля температур в среде, как следует из (1.4.44) – (1.4.50), необходимо задание функции плотности радиоактивного загрязнителя. Постановка этой задачи осуществлена в пункте 1.5, а её решению посвящена глава II.
1.3.3. Постановка задачи теплопереноса в первом приближении
Уравнения (1.4.27), (1.4.28) для коэффициентов при ![]() (первое приближение) принимают вид
(первое приближение) принимают вид
|
|
(1.4.51) |
|
|
(1.4.52) |
Для коэффициентов при ![]() в (1.4.29)
в (1.4.29)
|
|
(1.4.53) |
Условия сопряжения, начальные и граничные условия
|
|
(1.4.54) |
|
|
(1.4.55) |
|
|
(1.4.56) |
|
|
(1.4.57) |
|
|
(1.4.58) |
Решение ![]() отыскивается в виде квадратного многочлена относительно z (1.4.43), где
отыскивается в виде квадратного многочлена относительно z (1.4.43), где ![]() и
и ![]() определяются как (1.4.41), (1.4.42), а значение
определяются как (1.4.41), (1.4.42), а значение ![]() предстоит найти.
предстоит найти.
Уравнения (1.4.51) – (1.4.58) определяют постановку задачи теплообмена в первом приближении. Здесь ![]() также зависит от плотности загрязнителя, что обусловливается выражениями для
также зависит от плотности загрязнителя, что обусловливается выражениями для ![]() ,
, ![]() .
.
1.5. Задача массопереноса
1.5.1. Математическая постановка задачи массопереноса и её обезразмеривание
Геометрия задачи массопереноса практически ничем не отличается от температурной задачи и представлена на рис. 1.2.
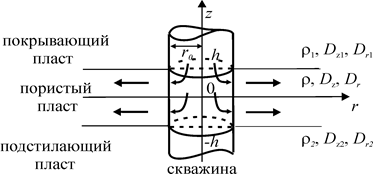
|
Рис. 1.2. Геометрия задачи массопереноса |
Математическая постановка задачи массопереноса для всех областей включает уравнение диффузии с учётом радиоактивного распада в покрывающем
|
|
(1.5.1) |
и подстилающем
|
|
(1.5.2) |
пластах, а также уравнение конвективной диффузии с учётом радиоактивного распада в пористом пласте
|
|
(1.5.3) |
При этом граничные условия включают в себя равенства плотностей и потоков растворённого вещества на границах раздела пластов
|
|
(1.5.4) |
|
|
(1.5.5) |
Плотность загрязнителя в скважине, радиус которой мы считаем малым по сравнению с расстояниями до точки наблюдения, равна ![]() , т.е.
, т.е.
|
|
(1.5.6) |
В начальный момент времени полагаем плотность загрязнителя равной нулю
|
|
(1.5.7) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

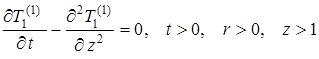 ,
, 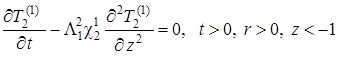 .
. 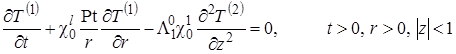 .
.  ,
, 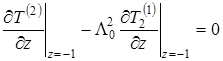 ,
,