Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
|
|
(1.4.12) |
а условия сопряжения, граничные и начальные условия принимают вид
|
|
(1.4.13) |
|
|
(1.4.14) |
|
|
(1.4.15) |
|
|
(1.4.16) |
|
|
(1.4.17) |
Уравнения и равенства (1.4.10) – (1.4.17) представляют математическую постановку задачи теплопереноса.
1.3.1. Разложение задачи теплопереноса по асимптотическому параметру
Рассмотрим более общую задачу, получающуюся введением произвольного асимптотического параметра ![]() путем формальной замены
путем формальной замены ![]() на
на ![]() и, соответственно,
и, соответственно, ![]() на
на ![]() , а
, а ![]() на
на ![]() . Задача (1.4.10) – (1.4.17) является, таким образом, частным случаем более общей задачи при
. Задача (1.4.10) – (1.4.17) является, таким образом, частным случаем более общей задачи при ![]() .
.
|
|
(1.4.18) |
|
|
(1.4.19) |
|
|
(1.4.20) |
|
|
(1.4.21) |
|
|
(1.4.22) |
|
|
(1.4.23) |
|
|
(1.4.24) |
|
|
(1.4.25) |
Будем искать решение задачи (1.4.18) – (1.4.25), разлагая каждое ![]() в ряд по параметру
в ряд по параметру ![]() . При этом асимптотические формулы с остаточным членом для данных разложений имеют вид
. При этом асимптотические формулы с остаточным членом для данных разложений имеют вид
|
|
(1.4.26) |
Решение исходной задачи будет получено из решения параметризованной задачи при ![]() . Подставив (1.4.26) в (1.4.18) – (1.4.25) и сгруппировав слагаемые по степеням параметра разложения
. Подставив (1.4.26) в (1.4.18) – (1.4.25) и сгруппировав слагаемые по степеням параметра разложения ![]() , получим следующую постановку параметризованной задачи (вместе с граничными условиями)
, получим следующую постановку параметризованной задачи (вместе с граничными условиями)
|
|
(1.4.27) |
|
|
(1.4.28) |
|
|
(1.4.29) |
|
|
(1.4.30) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

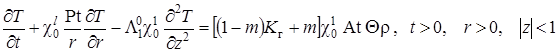 ,
, 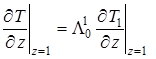 ,
, 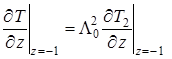 ,
, 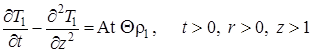 ,
, 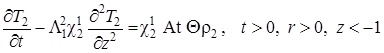 ,
, 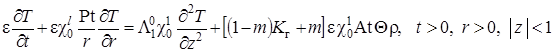 ,
, 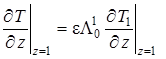 ,
, 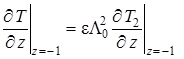 ,
, 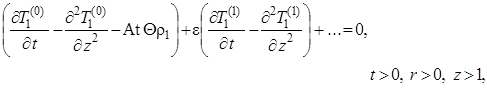
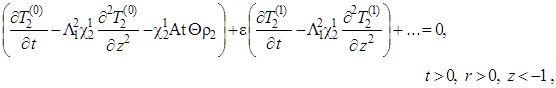
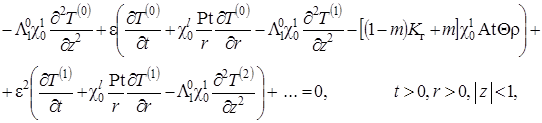
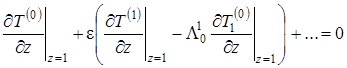 ,
,
 ,
,