Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
|
|
(1.4.31) |
|
< img width=195 height=40 src="images/referats/13436/image161.png">, |
(1.4.32) |
|
|
(1.4.33) |
|
|
(1.4.34) |
При этом плотность загрязнителя, входящая в (1.4.27) – (1.4.29), также будет разлагаться по параметру асимптотического разложения ![]() , причём это разложение производится независимо от разложения (1.4.26), хотя и по тому же принципу.
, причём это разложение производится независимо от разложения (1.4.26), хотя и по тому же принципу.
1.3.2. Математическая постановка задачи теплопереноса в нулевом приближении
Из (1.4.29) для коэффициентов при ![]() (нулевое приближение) получим
(нулевое приближение) получим ![]() , тогда
, тогда ![]() . Таким образом, в нулевом приближении температура загрязнителя является функцией только от r и t. Из условий сопряжения (1.4.30)
. Таким образом, в нулевом приближении температура загрязнителя является функцией только от r и t. Из условий сопряжения (1.4.30) ![]() . Следовательно, температура загрязнителя в каждом вертикальном сечении одинакова по всей высоте несущего пласта
. Следовательно, температура загрязнителя в каждом вертикальном сечении одинакова по всей высоте несущего пласта ![]() . Приравнивая коэффициенты при
. Приравнивая коэффициенты при ![]() к нулю в уравнении (1.4.29), получим
к нулю в уравнении (1.4.29), получим
|
|
(1.4.35) |
Сумму первых двух слагаемых в правой части этого уравнения, не зависящую от z, обозначим через ![]()
|
|
(1.4.36) |
Тогда
|
|
(1.4.37) |
следовательно,
|
|
(1.4.38) |
При z = 1, воспользовавшись (1.4.30)
|
|
(1.4.39) |
при z = – 1
|
|
(1.4.40) |
Вычитая и складывая два последних уравнения, получим для функций ![]() и
и ![]() следующие выражения:
следующие выражения:
|
|
(1.4.41) |
|
|
(1.4.42) |
Проинтегрировав (1.4.38), получим
|
|
(1.4.43) |
здесь ![]() функция, не зависящая от z, значение которой предстоит найти.
функция, не зависящая от z, значение которой предстоит найти.
Подставив выражение ![]() из (1.4.41) в (1.4.36), получим для нулевого приближения уравнение гиперболического типа со следами производных из внешних областей
из (1.4.41) в (1.4.36), получим для нулевого приближения уравнение гиперболического типа со следами производных из внешних областей
|
|
(1.4.44) |
Окончательная постановка задачи в нулевом приближении наряду с (1.4.44) включает также уравнения для окружающих сред, начальные, граничные условия и условия сопряжения
|
|
(1.4.45) |
|
|
(1.4.46) |
|
|
(1.4.47) |
|
|
(1.4.48) |
|
|
(1.4.49) |
|
|
(1.4.50) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

 .
. 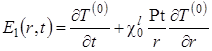 .
. 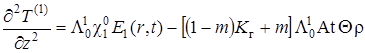 ,
, 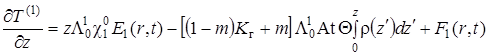 .
. 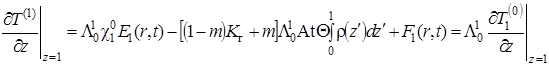 ,
, 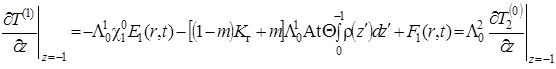 .
. 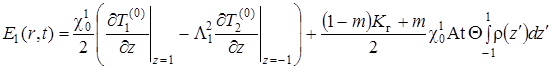 ,
, 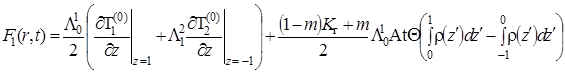 .
. 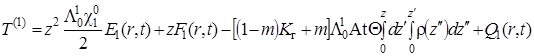 ,
, 
 ,
, 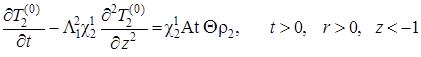 ,
,