Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты

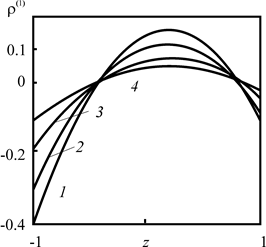
Рефераты / Физика и энергетика / Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты

Рисунок 2.23 показывает зависимость от вертикальной координаты в случае различия коэффициентов диффузии надстилающего и подстилающего пластов. Симметрия относительно z = 0 нарушается, более высокий коэффициент определяет и большее абсолютное значение . С увеличением

расстояния до оси скважины происходит «сглаживание» .

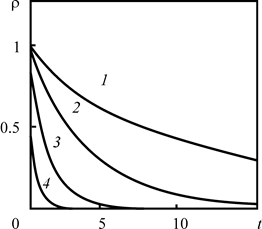
Из рис. 2.24 следует, что при малых постоянных распада различие между первым и нулевым приближениями остаётся практически постоянным, в то время, как при больших At уменьшение плотности загрязнителя за счёт распада становится преобладающим и разница между нулевым и первым приближениями уменьшается.

Рис. 2.23. Зависимость коэффициента первого приближения плотности радиоактивных примесей от z для безразмерного времени t = 10 на «относительных расстояниях» от оси скважины: 1 – R = 0.2, 2 – 0.4, 3 – 0.6, 4 – 0.8. Графики построены для At = 0.3. Другие расчётные параметры Pd = 102, , , ,

Рис. 2.24. Зависимость плотности радиоактивного загрязнителя в нулевом (1, 3) и первом (2, 4) приближениях от «относительного расстояния» для различных постоянных распада 1,2 – At = 0.1, 3,4 – 1. Графики построены для t = 10. Другие расчётные параметры Pd = 102, , ,

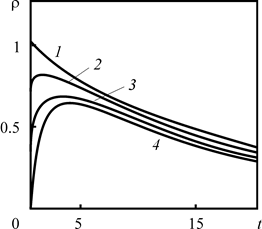
Анализ рис. 2.25 показывает, что с увеличением времени кривые, отвечающие плотности загрязнителя в различных горизонтальных плоскостях, приближаются друг к другу, что вызвано, прежде всего, уменьшением в результате радиоактивного распада.

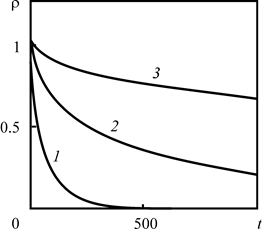
На рис. 2.26 представлена зависимость плотности загрязнителя при отсутствии радиоактивного распада от времени. При этом уменьшение определяется только процессами диффузии. Чем больше величина , т.е. чем ближе по абсолютной величине коэффициент диффузии к коэффициенту температуропроводности, тем быстрее уменьшается плотность, и наоборот.

Рис. 2.25. Зависимость плотности радиоактивного загрязнителя в первом приближении от времени для различных z: 1 – z = 0.5, 2 – 0.7, 3 – 0.9, 4 – 1. Графики построены для R = 0.5. Другие расчётные параметры At = 0.3, Pd = 102, , ,

Рис. 2.26. Зависимость плотности нерадиоактивного загрязнителя в первом приближении от времени для различных : 1, 2 – , 3 – . Графики построены для R = 0.9 и z = 0.5. Другие расчётные параметры At = 0, Pd = 102, ,

При наличии радиоактивного загрязнителя картина в большей степени определяется процессами радиоактивного распада, что хорошо видно на рис. 2.27. Особенно существенна разница в масштабе оси времени между 2.26 и 2.27, что вызвано большим временем «диффузионной релаксации» в сравнении со средним временем жизни нуклида.

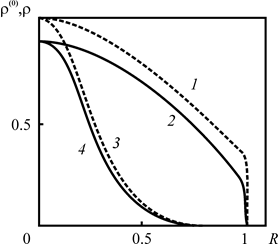
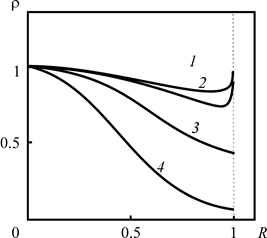
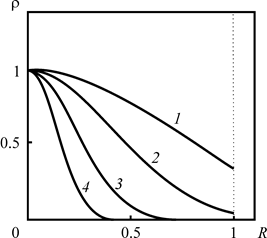
Из рис. 2.28, 2.29 следует, что увеличение времени закачки приводит к «сглаживанию» плотности загрязнителя в первом приближении на границе зоны загрязнения, что позволяет в этом приближении получать хорошие результаты для всех постоянных распада и на всех расстояниях.

Рис. 2.27. Зависимость плотности нерадиоактивного загрязнителя в первом приближении от времени для различных постоянных распада: 1 – At = 0.1, 2 – 0.3, 3 – 1, 4 – 3. Графики построены для R = 0.9 и z = 0.5. Другие расчётные параметры Pd = 102, , ,

Рис. 2.28. Зависимость плотности радиоактивного загрязнителя в первом приближении от расстояния до оси скважины, отнесённого к максимальному радиусу зоны загрязнения для безразмерного времени t = 1. При различных постоянных распада: 1 – At = 0.1, 2 – 0.3, 3 – 1, 4 – 3. Графики построены для z = 0.5. Другие расчётные параметры Pd = 102, , ,

Рис. 2.29. Зависимость плотности радиоактивного загрязнителя в первом приближении от расстояния до оси скважины, отнесённого к максимальному радиусу зоны загрязнения для безразмерного времени t = 10. При различных постоянных распада: 1 – At = 0.1, 2 – 0.3, 3 – 1, 4 – 3. Графики построены для z = 0.5. Другие расчётные параметры Pd = 102, , ,

Скачать реферат

Страница: 1  2  3  4  5  6  7  8  9  10  11  12  13  14  15
16  17  18  19  20  21  22  23  24  25  26  27  28  29  30
31  32  33  34  35  36  37  38  39

Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты

Другие рефераты на тему «Физика и энергетика»:

Поиск рефератов

Последние рефераты раздела