Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
|
|
(1.5.27) |
|
|
(1.5.28) |
|
|
(1.5.29) |
Будем искать решение задачи (1.5.22) – (1.5.29), разлагая значение плотности ![]() каждой из областей в ряд по параметру
каждой из областей в ряд по параметру ![]() . При этом для данных разложений асимптотические формулы с остаточным членом имеют вид
. При этом для данных разложений асимптотические формулы с остаточным членом имеют вид
|
|
(1.5.30) |
Решение исходной задачи получается из решения параметризованной задачи при ![]() . Подставив выражения (1.5.30) в (1.5.22) – (1.5.29) и сгруппировав слагаемые по степеням параметра разложения
. Подставив выражения (1.5.30) в (1.5.22) – (1.5.29) и сгруппировав слагаемые по степеням параметра разложения ![]() , получим следующую постановку параметризованной задачи
, получим следующую постановку параметризованной задачи
|
|
(1.5.31) |
|
|
(1.5.32) |
|
|
(1.5.33) |
|
|
(1.5.34) |
|
|
(1.5.35) |
|
|
(1.5.36) |
|
|
(1.5.37) |
|
|
(1.5.38) |
Анализ постановки задачи показывает, что условия сопряжения (1.5.34) позволяют связать между собой решения разных приближений в пласте проводимости, “подошве” и “кровле”. Это и определяет возможность “расцепления” получающихся уравнений, содержащих коэффициенты разложения соседних порядков.
1.5.3. Математическая постановка задачи массопереноса в нулевом приближении
Приравнивая коэффициенты при сомножителях ![]() (нулевое приближение) в уравнении (1.5.33), получим
(нулевое приближение) в уравнении (1.5.33), получим
|
|
(1.5.39) |
а, следовательно, после интегрирования
|
|
(1.5.40) |
Таким образом, в нулевом приближении плотность загрязнителя является функцией только от r и t. Далее, из условий сопряжения (1.5.34) получаем ![]() . Следовательно, в нулевом приближении плотность загрязнителя в каждом вертикальном сечении одинакова по всей высоте несущего пласта
. Следовательно, в нулевом приближении плотность загрязнителя в каждом вертикальном сечении одинакова по всей высоте несущего пласта ![]() .
.
Приравнивая к нулю коэффициенты при ![]() в (1.5.33), получим
в (1.5.33), получим
|
|
(1.5.41) |
Левую часть этого уравнения, в силу вышеизложенного не зависящую от z, обозначим через ![]() :
:
|
|
(1.5.42) |
тогда
|
|
(1.5.43) |
Интегрируя это уравнение по z, получим
|
|
(1.5.44) |
Повторное интегрирование позволяет представить первый коэффициент разложения в виде квадратного трехчлена относительно z, коэффициенты которого являются функциями от радиальной переменной и времени, но не зависят от z
|
|
(1.5.45) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

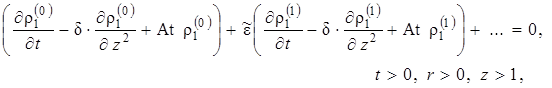
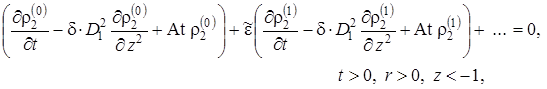
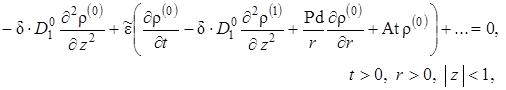
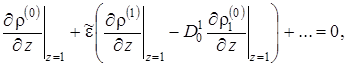
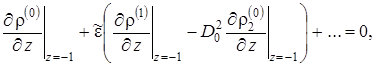
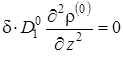 ,
, 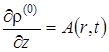 .
. 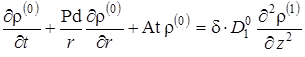 .
. 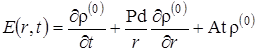 ,
, 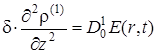 .
. 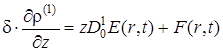 .
. 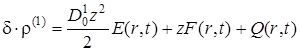 .
.