Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
Если при расчётах полагать, что ![]() , то на расстояниях до 0,9Rd для τ £300 лет погрешность бездиффузионного приближения не превышает 5%. Это позволяет во многих практических задачах использовать бездиффузионное приближение.
, то на расстояниях до 0,9Rd для τ £300 лет погрешность бездиффузионного приближения не превышает 5%. Это позволяет во многих практических задачах использовать бездиффузионное приближение.
Расстояние от скважины, на котором можно пользоваться бездиффузионным приближением, естественн
о назвать «радиусом бездиффузионного приближения». Аналогично можно ввести понятие «время бездиффузионного приближения».
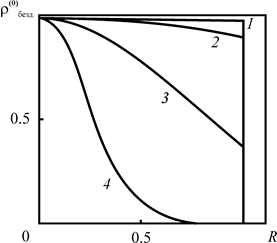
На рис. 2.10 приведены результаты расчётов плотности ![]() радиоактивных примесей для бездиффузионного приближения в зависимости от относительного расстояния до скважины. Параметр Pd при расчётах принимался равным 102.
радиоактивных примесей для бездиффузионного приближения в зависимости от относительного расстояния до скважины. Параметр Pd при расчётах принимался равным 102.
|
|
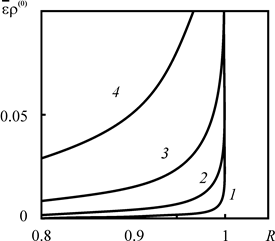
Рис. 2.10. Зависимость относительной погрешности бездиффузионного приближения от расстояния до оси скважины, отнесенного к радиусу зоны загрязнения, при различных временах закачки 1 – t = 0.1, 2 – 1, 3 – 10, 4 – 100. Pd = 102, |
Кривые, приведённые на рис. 2.11 рассчитаны для значения безразмерного времени t = 10. При отсутствии диффузии уменьшение концентрации загрязнителя происходит только в результате радиоактивного распада. Поэтому в случае Аt = 0 плотность ![]() постоянна па всём участке вплоть до фронта загрязнителя (положение которого задаётся функцией Хевисайда), где скачком падает до нуля (кривая 1). Вид кривых 2 – 4 определяется радиоактивным распадом.
постоянна па всём участке вплоть до фронта загрязнителя (положение которого задаётся функцией Хевисайда), где скачком падает до нуля (кривая 1). Вид кривых 2 – 4 определяется радиоактивным распадом.
|
|
Рис. 2.11. Зависимость плотности Pd = 102, |
2.4. Решение задачи массообмена в первом приближении
Выпишем ещё раз полученную в разделе 1.5.4 математическую постановку задачи массообмена для коэффициентов первого приближения, пренебрегая радиоактивным распадом в водоупорных пластах
|
|
(2.4.1) |
|
|
(2.4.2) |
|
|
(2.4.3) |
начальные условия, условия сопряжения и граничные условия
|
|
(2.4.4) |
|
|
(2.4.5) |
|
|
(2.4.6) |
|
|
(2.4.7) |
Напомним, что решение ![]() отыскивается в форме квадратного многочлена относительно z
отыскивается в форме квадратного многочлена относительно z
|
|
(2.4.8) |
где
|
|
(2.4.9) |
|
|
(2.4.10) |
Определение ![]() сводится к решению уравнения
сводится к решению уравнения
|
|
(2.4.11) |
где введён оператор
|
|
(2.4.12) |
Перейдём далее к пространству изображений (преобразование Лапласа – Карсона). При этом оператор ![]() принимает вид
принимает вид
|
|
(2.4.13) |
Выражение (2.4.11) в пространстве изображений
|
|
(2.4.14) |
Имеет смысл сначала найти в пространстве изображений выражения ![]() и
и ![]() . Воспользовавшись аналогами (2.4.9) и (2.4.10) в пространстве изображений, а также (2.1.48), (2.1.49), получим
. Воспользовавшись аналогами (2.4.9) и (2.4.10) в пространстве изображений, а также (2.1.48), (2.1.49), получим
|
|
(2.4.15) |
Другие рефераты на тему «Физика и энергетика»:
- Статистическая механика классических систем
- Содержание и структура тестовых материалов по механике
- Моделирование динамики яркостной температуры земли методом инвариантного погружения и нейронных сетей
- Особенности размещения и развития атомной энергетики РФ. Противоречия, перспективы
- Проектирование электрической сети
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

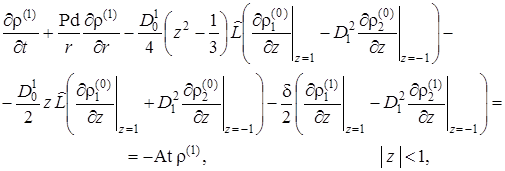
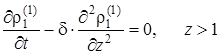 ,
, 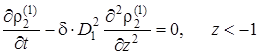 ,
, 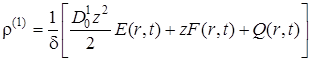 ,
, 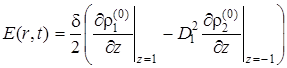 ,
, 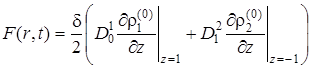 .
.  ,
, 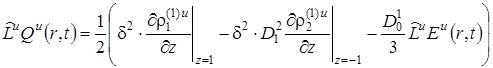 .
. 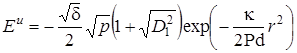 ,
,