Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
Последнее слагаемое в правой части уравнения (3.1.1) содержит сомножитель, определяемый плотностью радиоактивного загрязнителя, нахождение которой описано в главе II. В разделе 1.5.5 показано, что интеграл 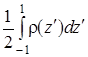 совпадает с нулевым приближением плотности
совпадает с нулевым приближением плотности ![]() и не зависит от
и не зависит от
![]() . Поэтому уравнение (3.1.1) можно переписать следующим образом
. Поэтому уравнение (3.1.1) можно переписать следующим образом
|
|
(3.1.7) |
Решение уравнения (3.1.2), с учётом граничных условий (3.1.6):
|
|
(3.1.8) |
Аналогично, для подстилающего пласта в пространстве изображений
|
|
(3.1.9) |
Учитывая условия сопряжения (3.1.4), эти решения можно переписать в виде
|
|
(3.1.10) |
|
|
(3.1.11) |
С помощью (3.1.10) и (3.1.11) выразим значения следов производных из внешних областей через температуру пласта в нулевом приближении
|
|
(3.1.12) |
Подставляя найденные значения производных (3.1.12) в уравнение (3.1.7), получим обыкновенное дифференциальное уравнение для определения температурного поля в пласте в нулевом приближении
|
|
(3.1.13) |
Введём обозначение для выражения, стоящего в квадратных скобках
|
|
(3.1.14) |
тогда
|
|
(3.1.15) |
Решение однородного уравнения, соответствующего (3.1.15) имеет вид
|
|
(3.1.16) |
Методом вариации произвольной постоянной определим ![]() .
.
|
|
(3.1.17) |
Для нахождения постоянной ![]() подставим (3.1.17) в (3.1.16) и учтём граничное условие (3.1.5), тогда
подставим (3.1.17) в (3.1.16) и учтём граничное условие (3.1.5), тогда
|
|
(3.1.18) |
Выражение для ![]() имеет вид
имеет вид
|
|
(3.1.19) |
а решение задачи в пласте в пространстве изображений представляется в форме
|
|
(3.1.20) |
С учётом (3.1.10), (3.1.11) температурное поле в окружающей среде описывается выражениями ( в пространстве изображений)
|
|
(3.1.21) |
|
|
(3.1.22) |
Для удобства перехода в пространство оригиналов перепишем (3.1.20) – (3.1.22) в виде
|
|
(3.1.23) |
|
|
(3.1.24) |
|
|
(3.1.25) |
Перейдем в пространство оригиналов, используя формулы обратного преобразования Лапласа – Карсона [23]
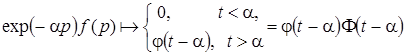 ,
,
где ![]() - единичная функция Хевисайда
- единичная функция Хевисайда
|
|
(3.1.26) |
|
|
(3.1.27) |
В нашем случае имеем
|
|
(3.1.28) |
|
где | |
|
|
(3.1.29) |
Другие рефераты на тему «Физика и энергетика»:
- Определение основных параметров пружинных импульсно-силовых узлов ручного механизированного инструмента
- Электроснабжение механического завода местной промышленности
- Автоматизация теплового пункта гражданского здания
- Нагревание воды и … экономический кризис
- Определение мощности судовой электростанции
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода


 ,
, 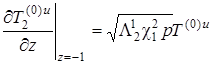 .
. 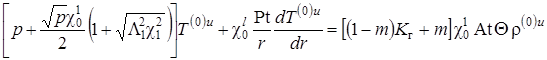 .
. 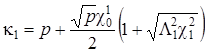 ,
,  .
.  .
. 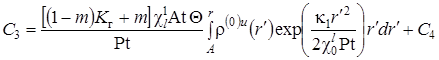 .
.  .
. 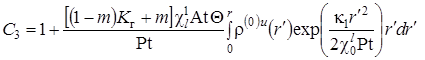 ,
, 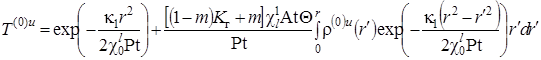 .
. 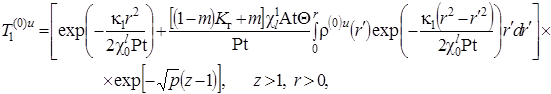
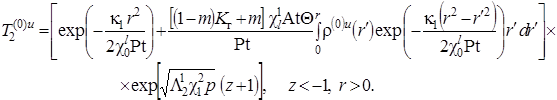 .
. 

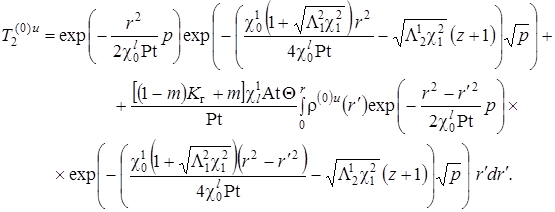
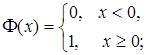
 ,
,  ,
, 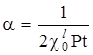 ,
,