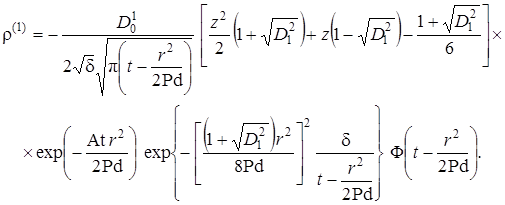Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
В нашем случае
|
|
(2.4.37) |
|
|
(2.4.38) |
Наконец, справедливо следующее соотношение
|
|
(2.4.39) |
Воспользовавшись (2.3.36) – (2.3.39), из (2.3.35) получим выражение для первого коэффициента разложения в форме
|
|
(2.4.40) |
При этом в первом приближении плотность загрязнителя представится как
|
|
(2.4.41) |
где ![]() и
и ![]() определяются выражениями (2.1.52) и (2.4.40).
определяются выражениями (2.1.52) и (2.4.40).
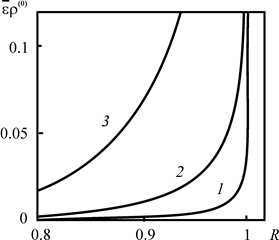
Оценим теперь вклад второго слагаемого в фигурных скобках выражения (2.4.40) по сравнению с первым. Полагая коэффициенты диффузии надстилающего и подстилающего пластов равными, для отношения этих слагаемых получим
|
|
(2.4.42) |
Анализ рис. 2.12 позволяет сделать вывод о возможности пренебрежения вторым слагаемым в фигурных скобках (2.4.40) по сравнению с первым для всех практически значимых времён на расстояниях до 0.95Rd. Графики на рис. 2.12 построены для z = 0, но аналогичные результаты получаются и при других z, за исключением точек ![]() , в которых (2.4.42) обращается в бесконечность.
, в которых (2.4.42) обращается в бесконечность.
|
|
Рис. 2.12. Зависимость |
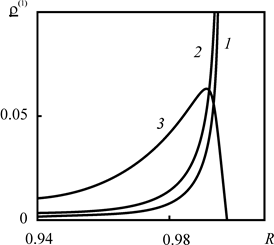
Однако из рис. 2.13 видно, что и в этом случае (в силу абсолютной малости соответствующего слагаемого) им можно пренебречь для расстояний меньших 0.98Rd. поэтому в дальнейшем при рассмотрении первого коэффициента асимптотического разложения ![]() будем полагать, что
будем полагать, что
|
|
Рис. 2.13. Зависимость второго слагаемого по раскрытии всех скобок в (2.4.40) от расстояния до оси скважины, отнесенного к радиусу зоны загрязнения, при различных временах закачки 1 – t = 10, 2 – 30, 3 – 100. Графики построены для |
|
|
(2.4.43) |
Выражение (2.4.43) с высокой степенью точности определяет первый коэффициент модифицированного асимптотического разложения плотности радиоактивного загрязнителя.
2.5. Анализ результатов расчетов в первом приближении
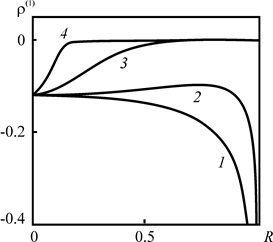
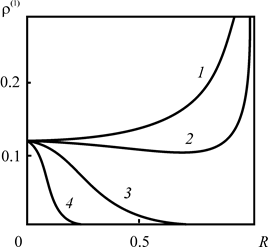
На рис. 2.14 и 2.15 представлены графики зависимости первого коэффициента разложения ![]() от расстояния до оси скважины. Вид графиков для z = 0 и z = 1 оказывается похожим, но «опрокинутым». При этом наиболее существенный вклад первого приближения наблюдается на границе зоны заражения.
от расстояния до оси скважины. Вид графиков для z = 0 и z = 1 оказывается похожим, но «опрокинутым». При этом наиболее существенный вклад первого приближения наблюдается на границе зоны заражения.
|
|
Рис. 2.14. Зависимость плотности |
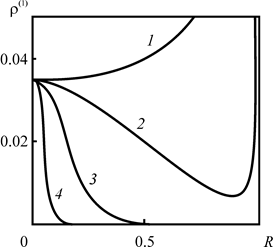
Сравнивая графики, представленные на рис. 2.15 и 2.16, приходим к выводу, что с увеличением времени, прошедшего с момента закачки, вклад ![]() уменьшается.
уменьшается.
|
|
Рис. 2.15. Зависимость плотности |
|
|
Рис. 2.16. Зависимость плотности |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

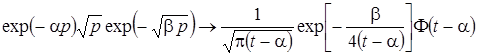 ,
,  .
. 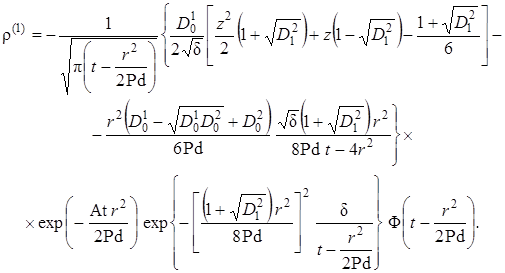
 .
.