Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты

Об этом же говорит и анализ рис. 2.17, на котором приведена зависимость первого коэффициента плотности радиоактивного загрязнителя от времени закачки на различных расстояниях от оси скважины. Причём, на бóльших расстояниях от оси уменьшение происходит быстрее.

Однако из рис. 2.18 следует, что для нерадиоактивных примесей имеет большое значение и на бóльших расстояниях от скважины. Следовательно, наблюдавшееся на рис. 2.17 различие в быстроте уменьшения определяется не столько диффузионными характеристиками, сколько радиоактивным распадом.

На рис. 2.19 представлена зависимость от расстояния до оси скважины, отнесённого к максимальному радиусу загрязнения. Различные кривые соответствуют разным расстояниям вдоль вертикальной координаты в пласте. Графики построены для безразмерного времени t = 3. При этом данное отношение не зависит от параметра At радиоактивного распада. Видно, что для столь незначительного времени на расстояниях вклад первого коэффициента приближения является весьма существенным.

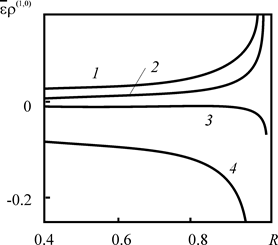
Анализ рис. 2.20, определяющего зависимость от расстояния до оси скважины, отнесённого к максимальному радиусу загрязнения, в сравнении с рис. 2.19, позволяет сделать вывод об уменьшении роли с ростом времени закачки. Графики построены для безразмерного времени t = 30, что соответствует размерному времени ~ 100 лет. При этом на расстояниях до вклад по сравнению с для горизонтов –0.6 < z < 0.6 весьма мал и составляет 3 – 5%.

Этот вывод подтверждается и анализом рис. 2.21, на котором представлена зависимость от времени. При увеличении времени закачки уменьшается относительный вклад . Следовательно, при значительных расчётных временах, распределение плотности загрязнителя описывается с высокой степенью точности нулевым приближением.

На рис. 2.22 представлена картина зависимости от вертикальной координаты. Коэффициенты диффузии надстилающего и подстилающего пластов полагаются одинаковыми. Картина симметрична относительно z = 0. при этом с увеличением расстояния до оси скважины происходит «сглаживание» значений .

 Скачать реферат