Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
Математическая постановка задачи теплопереноса для всех областей, таким образом, включает уравнение теплопроводности с учётом радиоактивного распада в покрывающем
|
|
(1.4.1) |
и подс
тилающем
|
|
(1.4.2) |
пластах, а также уравнение конвективного переноса с учётом радиоактивного распада в пористом пласте
|
|
(1.4.3) |
Сомножитель при ![]() во втором слагаемом в левой части уравнения (1.4.3) в развёрнутом виде
во втором слагаемом в левой части уравнения (1.4.3) в развёрнутом виде
|
|
Условия сопряжения включают в себя равенство температур
|
|
(1.4.4) |
и потоков тепла на границах раздела пластов
|
|
(1.4.5) |
В уравнениях (1.4.1) – (1.4.3) учтено, что плотность радиоактивного нуклида в данной точке пространства определяется суммой плотностей в носителе и в скелете, которые связаны соотношением (1.3.4).
В начальный момент времени температура пластов ![]() является естественной невозмущённой температурой Земли на данной глубине. Рассматривая глубины, превышающие порог влияния сезонных температур (~100 м), будем считать, что в силу малой величины градиента температурного поля Земли (~0.01 К/м) и небольшой толщины пористого пласта (~10 м)
является естественной невозмущённой температурой Земли на данной глубине. Рассматривая глубины, превышающие порог влияния сезонных температур (~100 м), будем считать, что в силу малой величины градиента температурного поля Земли (~0.01 К/м) и небольшой толщины пористого пласта (~10 м)
|
|
(1.4.6) |
Температура загрязнителя в скважине, радиус которой мы считаем малым по сравнению с расстоянием до точки наблюдения, равна ![]()
|
|
(1.4.7) |
Будем в дальнейшем искать превышение температуры в пластах над естественной температурой, выраженное в единицах геотермической температуры в пористом пласте ![]() .
.
При решении задачи удобно перейти к безразмерным координатам, определяемым соотношениями
|
|
(1.4.8) |
Сразу заметим, что в силу (1.3.7)
|
|
(1.4.9) |
Безразмерный параметр At представляет собой отношение времени тепловой релаксации слоёв к среднему времени жизни радиоактивного нуклида. Выражение Pt является аналогом параметра Пекле, поскольку определяется аналогично последнему, но через температуропроводность настилающего, а не несущего пласта. Величина ![]() определяет отношение изменения температуры, вызванного «мгновенным» распадом радиоактивного нуклида к разности температур закачиваемой жидкости и естественной геотермической температуры пласта.
определяет отношение изменения температуры, вызванного «мгновенным» распадом радиоактивного нуклида к разности температур закачиваемой жидкости и естественной геотермической температуры пласта.
Для больших ![]() температурное поле определяется в основном энергией радиоактивного распада, для малых – конвективным переносом тепла, обусловленного различием температур закачиваемой жидкости и пласта.
температурное поле определяется в основном энергией радиоактивного распада, для малых – конвективным переносом тепла, обусловленного различием температур закачиваемой жидкости и пласта.
В силу большого значения аналога параметра Пекле (Рt ~ ![]() ), в пористом пласте можно пренебречь радиальной кондуктивной теплопроводностью по сравнению с конвективным переносом тепла.
), в пористом пласте можно пренебречь радиальной кондуктивной теплопроводностью по сравнению с конвективным переносом тепла.
Аналогично, для настилающего и подстилающего пластов изменение радиальной составляющей температурного поля будет в значительной мере определяться конвективным переносом тепла в пористом пласте, что позволяет пренебречь для них вкладом соответствующих радиальных теплопроводностей.
Таким образом, во всех уравнениях, получающихся из (1.4.1) – (1.4.3) исчезнут слагаемые, содержащие ![]() и интересующие нас уравнения запишутся в виде (соответственно для настилающего, подстилающего и пористого пластов):
и интересующие нас уравнения запишутся в виде (соответственно для настилающего, подстилающего и пористого пластов):
|
|
(1.4.10) |
|
|
(1.4.11) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

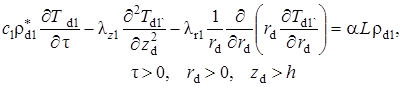
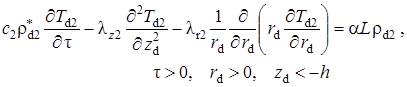
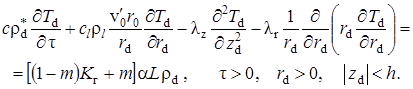
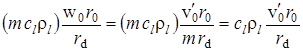 .
. 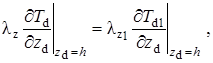
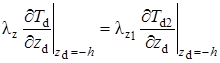 .
. 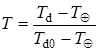 ,
, 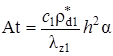 ,
, 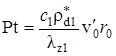 ,
,
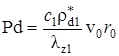 ,
, 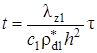 ,
, 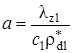 ,
, 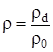 ,
,
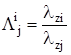 ,
, 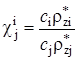 ,
, 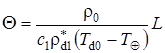 .
. 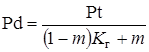 .
. 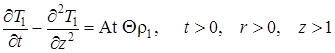 ,
, 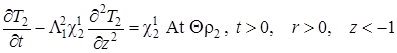 ,
,