Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
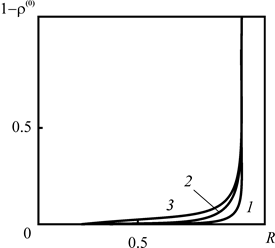
На рис 2.7 представлена зависимость вклада диффузионного массообмена с окружающей средой от расстояния до оси скважины, отнесенного к радиусу зоны загрязнения Rd. Из рисунка следует, что влияние диффузионного массообмена для больших времён (~10 лет) вблизи фронта загрязнения является весьма существенным. В расчетах приято Pd = 100, δ = 10-3, At = 0. Последнее соответствует пренебрежению
радиоактивным распадом.
|
|
Рис. 2.7. Вклад диффузионного массообмена с окружающей средой от расстояния до оси скважины, отнесенного к радиусу зоны загрязнения, при различных временах закачки: 1 – t = 0.1, 2 – 1, 3 – 10. At = 0, |
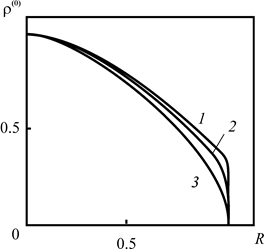
На рис 2.8 приведена зависимость плотности радиоактивного загрязнителя в нулевом приближении от расстояния до оси скважины, отнесенного к радиусу зоны загрязнения Rd для различных времён закачки и постоянных распада. Причём, значения t и At выбраны таким образом, что t∙At=1. При этом графики плотностей оказываются весьма близкими друг к другу. Различие между ними определяется лишь наличием диффузионных процессов. Это подчёркивает физическую разумность выбранной системы обезразмеривания.
|
|
Рис. 2.8. зависимость плотности загрязнителя (нулевое приближение) от расстояния до оси скважины, отнесенного к радиусу зоны загрязнения, при различных временах закачки и постоянных распада 1 – t = 0.1, At = 10, 2 – t = 10, At = 0.1, 3 – t = 100, At = 0.01, |
Если строить зависимость ![]() , то заметить «близость» графиков затруднительно, поскольку радиус зоны загрязнения растёт, согласно (2.1.55) пропорционально
, то заметить «близость» графиков затруднительно, поскольку радиус зоны загрязнения растёт, согласно (2.1.55) пропорционально ![]() .
.
2.3. Бездиффузионное приближение в задаче массообмена
В силу того, что отношение коэффициентов диффузии (![]() ) и температуропроводности (
) и температуропроводности (![]() ) является малой величиной порядка ~
) является малой величиной порядка ~ ![]() ÷
÷![]() (см. (1.5.12)), появляется возможность упростить взаимосвязанную задачу тепломассопереноса, рассмотрев бездиффузионное приближение, суть которого заключается в пренебрежении диффузионными слагаемыми в соответствующей задаче массопереноса.
(см. (1.5.12)), появляется возможность упростить взаимосвязанную задачу тепломассопереноса, рассмотрев бездиффузионное приближение, суть которого заключается в пренебрежении диффузионными слагаемыми в соответствующей задаче массопереноса.
Преимущество такого подхода в значительном упрощении процедуры построения решения тепломассообменной задачи. Однако, при использовании бездиффузионного приближения необходимо разрешение вопросов, связанных с оценкой его применимости.
Рассматривая найденное нами выражение для ![]() (2.1.52) как функцию от
(2.1.52) как функцию от ![]() , разложим его в ряд Маклорена по малому параметру
, разложим его в ряд Маклорена по малому параметру ![]() , причём ограничимся первыми двумя членами разложения
, причём ограничимся первыми двумя членами разложения
|
|
(2.3.1) |
Из (2.2.1), учитывая, что ![]() , получим
, получим
|
|
(2.3.2) |
Далее, вычислив производную
|
|
(2.3.3) |
и подставляя (2.3.2) и (2.3.3) в (2.3.1), окончательно получим
|
|
(2.3.4) |
В случае бездиффузионного приближения в уравнении (1.5.41) сразу пренебрегаем диффузионной составляющей, и оно принимает вид
|
|
(2.3.5) |
или, проведя преобразование Лапласа – Карсона, в пространстве изображений
|
|
(2.3.6) |
Решение этого уравнения (в пространстве оригиналов)
|
|
(2.3.7) |
что совпадает с нулевым приближением (по ![]() ) для задачи массопереноса с учётом вертикальной диффузии.
) для задачи массопереноса с учётом вертикальной диффузии.
Относительная погрешность, возникающая при пренебрежении вторым слагаемым в квадратных скобках в выражении (2.3.4), и определяет погрешность бездиффузионного приближения
|
|
(2.3.8) |
Анализ рис.2.9, на котором показана зависимость относительной погрешности бездиффузионного приближения от расстояния до оси скважины, отнесенного к радиусу зоны загрязнения, показывает, что за время ![]() ~30 лет погрешность данного приближения на расстояниях до 0,9Rd не превышает нескольких процентов и лишь для значительных времён
~30 лет погрешность данного приближения на расстояниях до 0,9Rd не превышает нескольких процентов и лишь для значительных времён ![]() ~300 лет, на расстояниях бóльших 0,7Rd становится существенной. Причём данные результаты не зависят от среднего времени жизни нуклида.
~300 лет, на расстояниях бóльших 0,7Rd становится существенной. Причём данные результаты не зависят от среднего времени жизни нуклида.
|
|
Рис. 2.9. Зависимость относительной погрешности бездиффузионного приближения от расстояния до оси скважины, отнесенного к радиусу зоны загрязнения, при различных временах закачки 1 – t = 0.1, 2 – 1, 3 – 10, 4 – 100. Pd = 102, |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

 .
. 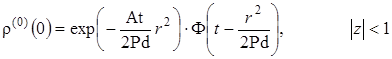 .
. 
 .
. 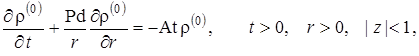
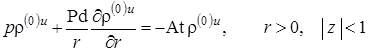 .
. 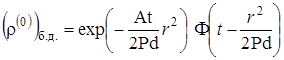 ,
, 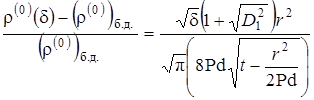 .
. 