Моделирование процессов тепло- и массопереноса при закачке радиоактивных растворов в глубокозалегающие пласты
|
|
(2.6.10) |
Будем искать решение задачи (2.6.4
) – (2.6.10) в виде асимптотического ряда по параметру ![]() , появляющемуся при формальной замене коэффициента диффузии
, появляющемуся при формальной замене коэффициента диффузии ![]() на частное
на частное ![]() . В соответствии с принятыми обозначениями это соответствует следующим заменам:
. В соответствии с принятыми обозначениями это соответствует следующим заменам:![]() , а
, а ![]() .
.
|
|
(2.6.11) |
Подставив выражения (2.6.11) в (2.6.4) – (2.6.10) и сгруппировав слагаемые по степеням параметра разложения ![]() , получим следующую постановку параметризованной задачи (вместе с граничными условиями)
, получим следующую постановку параметризованной задачи (вместе с граничными условиями)
|
|
(2.6.12) |
|
|
(2.6.13) |
|
|
(2.6.14) |
|
|
(2.6.15) |
|
|
(2.6.16) |
|
|
(2.6.17) |
|
|
(2.6.18) |
Приравнивая коэффициенты при ![]() в уравнении (2.6.14) и учитывая условие (2.6.15), получим, что в нулевом приближении плотность загрязнителя является функцией только от r, т.е. в каждом вертикальном сечении одинакова по высоте несущего пласта
в уравнении (2.6.14) и учитывая условие (2.6.15), получим, что в нулевом приближении плотность загрязнителя является функцией только от r, т.е. в каждом вертикальном сечении одинакова по высоте несущего пласта ![]() . Далее, приравняв к нулю коэффициенты при
. Далее, приравняв к нулю коэффициенты при ![]() в уравнении (2.6.14), получим
в уравнении (2.6.14), получим
|
|
(2.6.19) |
Левую часть этого уравнения, не зависящую от z, обозначим через ![]() :
:
|
|
(2.6.20) |
Тогда ![]() , следовательно
, следовательно
|
|
(2.6.21) |
|
|
(2.6.22) |
Здесь ![]() ,
, ![]() – неизвестные пока функции.
– неизвестные пока функции.
Из условий сопряжения (2.6.15) при сомножителе ![]() получим
получим
|
|
(2.6.23) |
|
|
(2.6.24) |
Тогда уравнение (2.6.20) примет вид
|
|
(2.6.25) |
Для нулевого приближения из (2.6.12) и (2.6.13) с учётом условий сопряжения (2.6.16)
|
|
(2.6.26) |
Продифференцировав последние выражения и подставив результат в (2.4.25), получим
|
|
(2.6.27) |
Решение этого уравнения представим как
|
|
(2.6.28) |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода

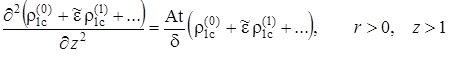 ,
, 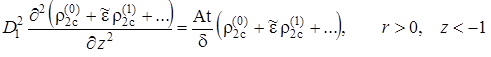 ,
, 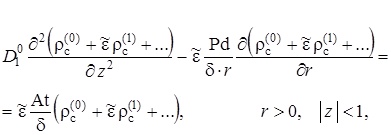
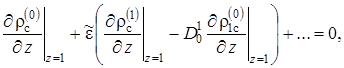
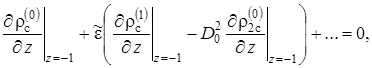
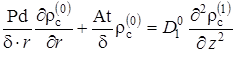 .
. 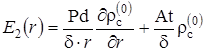 .
. 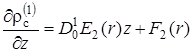 ,
, 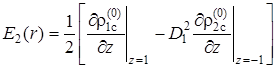 ,
, 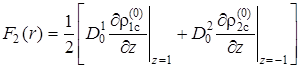 .
. 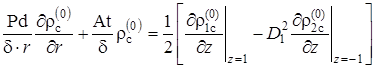 .
. 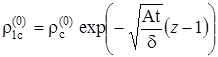 ,
, 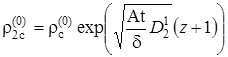 .
. 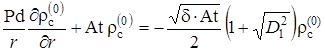 .
. 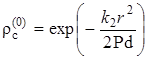 ,
,