Моделирование рабочих процессов погрузочно-транспортных модулей с учетом случайного характера внешних воздействий

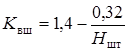, (3.2)

где Квг – коэффициент, учитывающий влияние вида груза; Ктп – коэффициент, характеризующий «трудности» процесса погрузки, то есть состояния почвы, разрыхлённость горной массы после взрыва; А – угол наклона передней кромки боковой стенки к почве выработки

, рад.; С1 – угол отклонения боковых стенок от вертикали, рад.; (S – S1) – глубина внедрения боковых стенок, см; S1 – длина выступающей части днища относительно боковых стенок, см; a – угол наклона почвы выработки к горизонту, град (a >0 при проведении уклонной выработки сверху вниз).

Коэффициент влияния угла сопряжения Кус по результатам экспериментальных исследований О.Д. Гагина [52] имеет вид:

, (3.3)

где С – угол сопряжения боковых стенок с днищем.

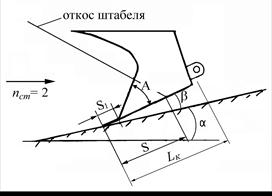
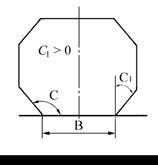
Геометрические параметры ковшей приведены на рисунке 3.1.

а)

б)

Рис. 3.1. Геометрические характеристики ковша:

а) машина с осевой разгрузкой ковша; б) машина с боковой разгрузкой ковша

Зависимость (3.1) является обобщением многолетних экспериментальных исследований, выполненных в научных школах СО АН СССР под руководством проф. Г.В. Родионова и в НПИ под руководством доцентов О.П. Иванова и В.Г. Сильня [32, 49]. Однако для современных ковшовых погрузочных машин её использование затруднительно по следующим соображениям:

1) используются внесистемные единицы измерения;

2) ковши машин с боковой разгрузкой могут не иметь боковых стенок или могут снабжаться одной боковой стенкой; в этом случае коэффициент Кус, учитывающий объединение зон деформаций на сопряжение днища и боковых стенок, должен учитывать реальную геометрическую форму ковша;

3) единое выражение для Wвн.к при и затрудняет использование формулы при программных вычислениях;

4) уточнить значения коэффициентов Квш в функции глубины внедрения.

Поэтому ниже приводятся результаты модификации выражения (3.2), выполненные путём разделения сопротивления внедрению днища Wвн.дн и боковых стенок Wвн.бок:

Wвн.к = Wвн.дн + Wвн.бок. (3.4)

Для формирования Wвн.дн. в первую часть выражения (3.1) введены следующие изменения, не противоречащие результатам экспериментальных исследований:

1) для днища Kус = 0,8; это значение соответствует ковшу без боковых стенок (при A = 70о, C = 120о);

2) коэффициент, учитывающий вид груза, Kвг, представлен в виде непрерывной функции [37]: для пород угольной формации при плотности породы в разрыхлённом состоянии rм £ 1500 кг/м3 и(или) f £ 10 единиц по шкале проф. М.М. Протодьяконова:

Kвг = 0,012 + 0,014 f , (3.5)

при rм > 1500 кг/м3 и f > 10

Kвг = 0,05 (rм × Kp × 10-3 – 0,4), (3.6)

где Kp – коэффициент разрыхления;

3) ширина ковша B, глубина внедрения S, размеры куска dэфф. – выражены в метрах, угол b1 – в градусах.

После преобразований математическая модель сопротивлений внедрению днища ковша имеет вид:

Wвн.дн.= 0,8 × 106 [B (dэфф. S + S2)] × × Kвш × Kвг × Kтп, (3.7)

где [Wвн.дн.]=Н; [B] = [dэфф.] = [S] = м; = 0,25+0,006b1; [b1] = град; (3.8)

Kвш – определяется формулой (3.2); Kвг – (3.5) или (3.6).

Математическая модель сопротивлений внедрению боковых стенок:

Wвн.б.ст = 10 nст × 0,12 ×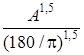

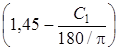× dcp (S – S1)2 × × Кус × Ктп × Квш × Квт × 106,

где nст – количество боковых стенок ковша, nст = 0; 1; 2; Кncт – коэффициент, учитывающий число боковых стенок ковша: при nст = 2, Кnст = 1; при nст = 1, Кnст = 0,65; [a] = [A] = [C1] = град; [S] = [S1] = [dcp] = м.

Коэффициенты Кус, Квш, Квг определяются, как и для днища, по формулам (3.2), (3.3), (3.5), (3.6).

После приведения постоянных формула для расчёта Wвн.б.ст имеет вид:

Wвн.б.ст = 1,2 ×106 × nст × dcp(S – S1)2 × 20,1α КA × КС1 × Кус ×

× Квш × Квг × Кnст × Ктп, (3.9)

где КА = 23 ×10-4 × А1,5; (3.10)

КС1 = 1,45 – 0,0175С1. (3.11)

Теперь объединённую математическую модель сопротивлений внедрения ковша произвольной формы в штабель можно представить в виде:

– при 0 < S < S1

Wвн = 0,8 × 106 [B(dcpд S + K'b1 S2)] × 20,1a Квш × Квг × Ктп ; (3.12)

– при Lк ≥ S ≥ S1

Wвн = 0,8 × 106{[ B(dcpд S + K'b1 S2)]+ 1,2 nст dcpб (S – S1)2×

× КA × Кус × КС1 × Кnст} × 20,1a × Квш × Квг × Ктп. (3.13)

В формулах dcpд и – средние размеры кусков перед днищем и боковой стенкой.

В целях оценки адекватности модели Wвн.(S) экспериментальным данным построены по формулам (3.12), (3.13) и коэффициентам (3.2) –Квш; (3.3) – Кус; (3.5) – Квг; (3.8) – К¢b1; (3.10) – КА; (3.11) – Кс1; Ктп – по условию трудности погрузки; Кnст – по числу боковых стенок зависимости Wвн.=f(S); 0 £ S £ Lк для ковшей машин 1ППН-5, МПК-3, МПК-1000Т (рис. 3.2).

а) б)

Рис. 3.2. Оценка адекватности зависимости по экспериментальным данным: а) зависимости Wвн(S) для пород различной крепости (f Î 7; 10; 13),

– экспериментальные данные; б) зависимости Wвн(S) для ковшей различных форм ковшовых машин: B = 1 м; f = 10

Программа и результаты расчёта выполнены в среде MathCad. Предварительное сопоставление расчётных и экспериментальных данных свидетельствует о приемлемой сходимости; количественные значения ошибок в определении средних значений приводятся ниже (п. 3.6).

Вопросам динамики внедрения ковша в штабель посвящены исследования О.П. Иванова [43], Б.П. Семко [66], Г.Ш. Хазановича [55] и других авторов. Вместе с тем, все эти работы выполнены для ковшовых машин на колёсно-рельсовом ходу. Для построения общих математических моделей расчёта глубины внедрения необходимо обобщение известных методов на машины с гидроприводом, оценка точности различных методических подходов.

 Скачать реферат