Моделирование рабочих процессов погрузочно-транспортных модулей с учетом случайного характера внешних воздействий

Глубина внедрения ковша в штабель Sк определяется в общем случае как результат решения дифференциальных уравнений движения погрузочной машины (поступательное движение) и ходового привода [55]:

(3.14)

(3.15)

где mм – масса погрузочной машины, кг; mв – масса прицепной части, например, вагонетки, кг; – угол наклона почвы выработки; м – скорость машины, м/с; Тсц – сила сцепления двигателя с основанием (рельсами, почвой), Н; Wвн(S) – сопротивление внедрению в функции глубины внедрения, Н; Мс – момент сопротивлений от ходовых перемещений машины, вагонетки, потерь в редукторе, Н×м; Jпр – приведённый к оси двигателя (колёса, звёздочки гусеничного механизма) момент инерции вращающихся масс – двигатель, редуктор, колёса и т.д., Н×мс2; wк – угловая скорость колеса, звёздочки, 1/с; Мqк – приведённый к оси движителя момент, развиваемый двигателем хода, Н×м.

Процесс внедрения состоит в общем случае из двух этапов:

1) движение без пробуксовки колёс относительно рельсов или гусениц относительно почвы с выключенным двигателем до достижения предельной силы сцепления Тсц;

2) движение после достижения Тсц предельной величины, после чего-либо возникает пробуксовка движителя с включённым двигателем хода, либо происходит отключение двигателя, и машина продолжает движение с реализацией кинематической энергии системы.

Решение системы уравнений (3.14), (3.15) позволяет получить зависимость S = f(t), где S – перемещение машины и, следовательно, ковша, t – время процесса. Для решения уравнений необходима информация о погрузочной машине (mм), прицепленной вагонетке (mв), законе сопротивлений внедрению ковша в штабель (Wвн(S)), моментах инерции вращающихся масс Ji и коэффициентах приведения каждой массы к оси движителя, внешней характеристике двигателя в функции угловой скорости Мдк , предельной силе сцепления движителя с основанием Тсц, моментах приведённых сопротивлений Мс. Необходимы также начальные условия (при t = 0, S = 0, м =) и граничные условия при переходе от первого этапа внедрения ко второму.

Принципиально решение системы нелинейных дифференциальных уравнений (3.14), (3.15) возможно приближенными методами на ПК, например, в программе MathCad. Практические затруднения возникают при получении информации о моментах инерции и внешней характеристике ходового двигателя.

Рассмотрено решение системы (3.14), (3.15) для ковшовых погрузочных машин двух типов:

1) с осевой разгрузкой ковша, на колёсно-рельсовом ходу, с электромеханическим приводом (аналог 1ППН-5);

2) с боковой разгрузкой ковша, смонтированного на жёсткой рукояти, на гусеничном ходу, с электрогидравлическим приводом (аналог МПК-3).

Машины с боковой разгрузкой ковша, смонтированного на поворотной телескопической рукояти, на гусеничном ходу, с электрогидравлическим приводом (аналог МПК-1000Т) не рассматриваются в динамическом процессе внедрения, так как в этих машинах ходовой механизм используется для маневровых операций; внедрение производится в статическом режиме механизмом гидравлического независимого напора.

При отсутствии пробуксовки колёс (гусениц) система (3.14), (3.15) на 1-м этапе может быть представлена одним уравнением:

, (3.16)

где mу – приведённая к поступательному движению масса вращающихся частей привода (двигатель, шестерни, валы, колёса); Тдк – приведённая к поступательному движению внешняя характеристика двигателя; Wc – приведённое к поступательному движению сопротивление от ходовых перемещений и потерь в редукторе.

Применяя известный порядок построения Тдк(uм) на основе данных, приведённых в технической характеристике погрузочной машины, получим для случая линейной характеристики двигатели на рабочем участке:

Tдк = Aдк – Bдк ×uм; ; ;

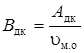Tдк.ном – номинальная сила тяги:

;

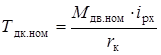мо – «синхронная» скорость движения машины:

.

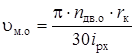Теперь уравнение (3.16) перепишем в виде:

mпр + Bдк × hрх+ Wвн(S) =

= Aдк × hрх – g(mм + mв) (w¢ cosa – sina), (3.17)

где mпр = (1 + Кj) × (mм + mв) – приведённая к поступательному движению масса системы, кг; mпост – масса поступательно движущихся частей, кг.

Уравнение (3.17) описывает процесс внедрения ковша в штабель на первом этапе, то есть до срыва колёс в пробуксовку. Начальные условия: t = 0; S = 0: 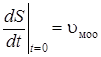. Величину можно найти из (3.17) при =0, Wвн(S) = 0, то есть .

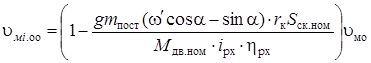Решение выполняется до S = S1, то есть до реализации глубины внедрения первого этапа. Условие окончания первого этапа: сила сцепления Тсц становится равной предельно допустимой, то есть Тсц.max = mм × g × y  cosa или

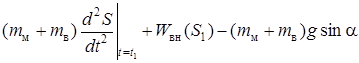
. (3.18)

Таким образом, при решении уравнения (3.17) в каждой точке t = ti определяется S = Si, , 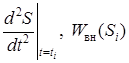и проверяется выполнение условия (3.18).

На втором этапе Тсц = Тсц.max, возникает избыточное скольжение колёс, сила сцепления остаётся постоянной и равной Тсц.max [57]. Нагрузка на двигатель сохраняется постоянной. Внедрение ковша описывается одним уравнением (3.14), которое теперь имеет вид:

. (3.19)

Если умножить левую и правую часть уравнения (3.19) на dS и проинтегрировать левую часть по u, а правую по S, то получим энергетическое соотношение:

. (3.20)

Графическая интерпретация решения представлена на рисунке 3.3. Решение уравнения (3.20) сводится к отысканию положения точки S2, в которой это условие выполняется.

 Скачать реферат