Моделирование рабочих процессов погрузочно-транспортных модулей с учетом случайного характера внешних воздействий

Таблица 2.3

Среднее долевое содержание фракций в объёме ковша в сравнении с аналогичным показателем штабеля

1-я реализация

2-я реализация

В реальных условиях случайный объём захвата Vкi,j, формируемый так, что разность между номинальным объёмом v и фактическим Vкi,j не превышает некоторой известной величины, то есть:

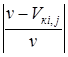£ e,

где – допустимая с позиций соотношения (v/Vк.max) относительная величина недогрузки или переполнения объёма v (Vк.max – объём куска максимального размера).

Значения могут устанавливаться путём статистических испытаний.

На начальном этапе при моделировании штабелей типа 1…5, = 0,05.

Если 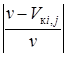> , то необходимо ввести процедуру корректировки гранулометрического состава материала, попавшего в объём v – догрузку при > 0, или разгрузку при < 0. Эта процедура должна проводиться поразрядно, так что величина разности принимается за исходный малый объём, в котором формируется как и для объёма v – число кусков, объём абсолютный и долевой каждого разряда.

Полученные значения суммируются алгебраически с числом кусков первого этапа моделирования, вычисляется суммарное число кусков, полный объём и долевое содержание.

Таким образом, получаем рекуррентный итеративный процесс моделирования гранулометрического состава внутри малого выделенного объёма до получения в каждом цикле моделирования условия £ e. Общий алгоритм приведён на рисунке 2.5. Результаты моделирования, выполненные согласно разработанному алгоритму, представлены в таблицах 2.4 и 2.5.

Как видно из приведённых данных, изменения суммарного объёма по фракциям стали менее значительными. Во всех реализациях относительные отклонения от номинального объёма не превысили 7,5 %, в подавляющем большинстве случаев ≤ 3,5 %. Такой уровень ошибки можно признать приемлемым.

Аналогичным образом отразилось использование корректирующего алгоритма на отклонение средних значений долевого содержания фракций в объёме ковша от математического ожидания. Величина составила при i = 0…7 не более 7,5 %, только в разрядах с крупными размерами кусков (dср8 = 0,51 м, dср9 = 0,57 м), отклонение составило 13,6 и 18,1 %, что вполне объяснимо.

Моделирование процесса «черпания» с последовательным уменьшением объёма штабеля выполнялось в соответствии с ранее изложенной программой. В отличие от процесса моделирования с постоянным объёмом и гранулометрическим составом, в этом случае после каждого «черпания», изменяется объём штабеля на величину vj – случайный объём единичного захвата. Оставшийся объём штабеля имеет новый, изменённый гранулометрический состав, характеризуемый долевым содержанием каждой фракции i ,j+1.

Алгоритм моделирования, приведённый на рисунке 2.5, необходимо дополнить изменением гранулометрического состава штабеля после очередного черпания и контролем завершения процесса при условии, что остаточный объём штабеля Vj < v¢. Общая структура алгоритма выгрузки штабеля последовательными черпаниями, номинальный объём которых равен v, представлен на рисунке 2.6. Программа и результаты моделирования приведены в приложении 2.

 Скачать реферат