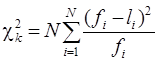Моделирование рабочих процессов погрузочно-транспортных модулей с учетом случайного характера внешних воздействий

2) формирование случайного потока единичных черпаний V(t) ковшовой погрузочной машиной за чистое время погрузки как совокупность моделей процессов внедрения, зачерпывания и наполнения ковша, а также продолжительность цикла;

3) формирование случайного грузопотока q(t) машиной с парными нагребающими лапами за чистое время погрузки как результат системного взаимодействия механизмов подачи, зах

вата материала лапами и устройства управления со штабелем;

4) преобразование случайного грузопотока дискретного V(t) или непрерывного q(t) призабойным транспортным оборудованием: перегружателем, средствами рельсового транспорта и т.п.;

5) наложение на грузопоток за чистое время погрузки затрат времени (и трудоёмкости) на выполнение вспомогательных операций и потока отказов и восстановлений для получения конечных показателей эффективности ППТМ за общее время работы.

2.2 Описание состава штабеля как функции случайной величины размера куска

В настоящее время традиционно состав штабеля по крупности слагающих его кусков di описывается с помощью приближённой гистограммы распределения, в которой указываются диапазоны разрядов и долевое содержание объёмов фракций. Например, так называемый рядовой штабель [44] имеет разряды (в м) – 0–0,1; 0,1–0,2; 0,2–0,4; 0,4–0,6 и соответствующее процентное содержание – 30; 30; 30; 10 (рис. 2.2). С помощью гистограммы можно определить средний размер куска dср в полном объёме штабеля. Такое представление состава штабеля недостаточно информативно и не позволяет с достаточной точностью решать задачу о гранулометрическом составе малого объёма v << V, где V – объём штабеля и, соответственно, о среднем размере куска в объёме v. Это, в свою очередь, препятствует разработке математических моделей процессов взаимодействия погрузочных и транспортирующих органов со штабелем при случайном изменении размера куска.

dmax = 0,6 м; х = d/dmax

		Кусочно-линейная функция распределения F*(х)

Рис. 2.2. Описание штабеля как функции случайной величины размера куска di

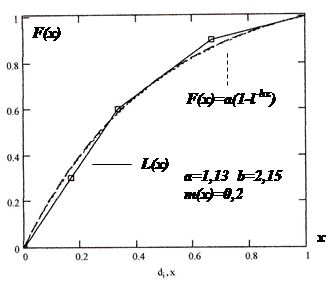
В реальном штабеле размер куска d – это непрерывная случайная величина, которая изменяется в пределах (0, dmax). Такое утверждение следует из того, что число кусков в штабеле достигает порядка 104. Поэтому состав штабеля логично представить в виде непрерывной функции F(d) (или плотности f(d)) распределения случайной величины d [93, 94].

Подбор аппроксимирующей кривой F(d) выполнен путём следующих преобразований экспериментальной гистограммы распределения (рис. 2.2):

1) в качестве случайной величины X выбрано отношение d/dmax, что позволило придать функции F(x) безразмерную форму;

2) по экспериментальным данным построена ступенчатая функция распределения , где – вероятность (частость) попадания случайной величины xn на соответствующий интервал;

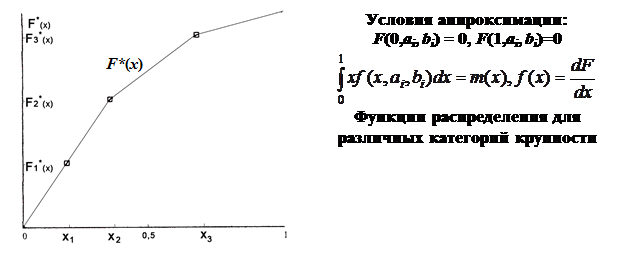
3) через точки А1, А2, …, Аn проведена теоретическая функция распределения F(x), удовлетворяющая условиям 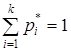; 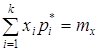, где mx – математическое ожидание случайной величины x = d/dmax;

4) соответствие теоретической функции распределения F(x) экспериментальным данным оценено с использованием критерия Пирсона – c2 [96].

По приведённой методике оценена степень приближения для ряда известных несимметричных функций распределения и показано, что наибольшей теснотой связи обладают логнормальное и экспоненциальное распределения. Последнее принято в качестве основного для дальнейших исследований. Функция распределения имеет вид: F(x) = a (1 – e –bx).

Значения коэффициентов a и b определялись в среде MathCad [98] по граничным условиям, заданной величине математического ожидания при минимальном среднеквадратическом отклонении искомой кривой от экспериментальных точек:

F(0) = 0; F = (1) = 1; ,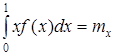

где ; .

Наряду с аппроксимацией гранулометрического состава рядового штабеля по экспериментальным данным при mx4=0,33, построены функции распределения крупности кусков «прогнозных» штабелей (рис. 2.2), в которых сохраняются или имеют симметричный вид функции распределения, но различаются средними размерами куска: mx1=0,5; mx2=0,67; mx3=0,75; mx5=0,25. Кривые F4(x) и F5(x) имеют экспоненциальный закон распределения, линия F1(x) – закон равномерной плотности F1(x) = x; кривые F2(x) и F3(x) построены как симметричные относительно линии F1(x) соответственно законам распределения F4(x) и F5(x):

 Скачать реферат