Моделирование рабочих процессов погрузочно-транспортных модулей с учетом случайного характера внешних воздействий

Анализ геометрических форм тел ссыпания и размеров ковша позволил выявить два принципиально различных случая (рис. 3.18):

1) ширина ковша такова, что объёмы ссыпания DV1 и DV2 не пересекаются; при этом ковш может быть заполнен на максимальную высоту lн;

2) ширина ковша Bк меньше Bк.min, объёмы ссыпания DV1 и DV2 пересекаются, максимально возможный уровень заполнения снижается до lQ. >Схема расчёта объёмов DV построена по унифицированному принципу. Все тела ссыпания представлены усечёнными призмами с основаниями в виде треугольников, для которых имеются достаточно простые методы вычисления объёмов.

На рисунке 3.18 и в приводимых ниже формулах обозначено: 1, 2, 3, 4 – участки торцевого сечения ковша, для которых определяются соответствующие площади F1…F4; Bк – ширина ковша; hст – высота задней стенки ковша; Sст – средняя длина боковой стенки ковша; к – угол отклонения днища ковша от вертикали в период перед разгрузкой ковша; Lкc – длина днища ковша; Lкcc – длина горизонтальная верхней стенки; c – угол ссыпания груза на открытых поверхностях; ¢c – угол ссыпания груза в стеснённой области между стенками ковша; lн, lQ – высота точки заполнения ковша для различных вариантов; DVк1 – объём ссыпания через открытую сторону ковша; DVк2 – то же через сторону ковша с боковой стенкой.

Случай 1. Максимальная вместимость ковша Vк.max:

- минимальная ширина, при которой объёмы ссыпания DV1 и DV2 не имеют общих зон:

, (3.49)

где lн – максимальное положение верхней точки заполнения:

lн = 0,5(hст × tgjc + Lксс (tgaк × tgjc + 1) + Lкс); (3.50)

- если Bк ³ Bк.min, то lн = lx и Vк.max определяется по формулам:

Vк.max = FSmax × Bк – DV1 – DV2; (3.51)

- максимальная площадь торцевой фигуры:

FSmax = F1 + F2 – F3 – F4; (3.52)

где F1= hст × lн; (3.53)

F2 = 0,5× tgaк; (3.54)

F3 = 0,5 (lн – lкс)2 × tgjc; (3.55)

F4 = 0,5 (lн – lксс)2 × (tgaк + ctgjc); (3.56)

- максимальные объёмы ссыпания:

; (3.57)

где i = 1 – открытая сторона ковша; i = 2 – сторона ковша с боковой стенкой;

; (3.58)

; (3.59)

; (3.60)

; (3.61)

- коэффициент потерь:

. (3.62)

Случай 2. Вместимость ковша Vк.max1 при Bк < Bк.min:

- уровень заполнения ковша грузом:

;

- оценка положения уровня груза относительно Lксс, Lкс и Sст, варианты:

(а) Lксс £ Lх < Lн; (б) Lкс £ Lх < Lксс;

(в) Sст £ Lх < Lкс; (г) 0 £ Lх < Sст;

- торцевая площадь:

(а) ; (б) ; (в) и (г) .

Площади F1…F4 определяются по (3.53) – (3.56) при lн = lQ:

- объёмы ссыпания:

а) DVi = DV1i + DV2i – DV3i – DV4i; б) DVi = DV1i + DV2i – DV3i;

в) и г) DVi = DV1i + DV2i.

Объёмы DV1i…DV4i определяются по (3.58) – (3.60) при lн = lQ.

Реальная вместимость ковша:

Vк.max1 = FS1 Bк. – DV1 – DV2.

Математические модели для расчёта фактического объёма груза, остающегося в ковше после черпания Vкз, коэффициент потерь п.

Общие соотношения

Vкз = Fзач Ксм Bк. – ,

где DV1 и DV2 – ранее определённые объёмы ссыпания через боковые стороны ковша; DV3 – объём, который не может поместиться в ковше из-за недостаточной вместимости:

DV3 = Fзач Ксм Bк. – Vк.max, при Bк. ³ Bк.min;

DV3 = Fзач Ксм Bк. – Vк.max1, при Bк. < Bк.min.

Объёмы DV1 и DV2 определяются по соотношениям (3.49) – (3.61) в зависимости от уровня заполнения ковша lx:

при Bк. ³ Bк.min и DV3 > 0 → lx = lн;

при Bк. < Bк.min и DV3 > 0 → lx = lQ.

Если DV3 < 0, то lx находится внутри диапазонов (а), (б), (в), (г). Конкретное значение lx определяется решением уравнения:

F(lx) = Fзач Ксм,

где F(lx) – торцевая площадь в зависимости от уравнения lx для вариантов (а), (б), (в), (г). Далее по унифицированным ранее приведённым моделям рассчитываются площади Fi и объёмы DVi,j.

Разработан алгоритм и программа в среде MathCad, позволяющая решать обе задачи (рис. 3.19). Программа построена так, что унифицированные операции вычисления площадей, объёмов ссыпания и уровня заполнения ковша выполняются отдельными подпрограммами.

Предлагаемая методика даёт возможность определить реальную вместимость ковша и фактический объём груза, остающийся в ковше после очередного черпания в функции глубины внедрения.

В целях проверки функционирования математических моделей и логики построения программы выполнен тестовый пример по анализу ковша машины МПК-3 (Bк = 1,0 м; Lксс = 1,1 м; Lкс = 0,85 м; hст = 0,6 м; Sст = 0,5 м; aк = 35о; jс = 45о; j¢с = 50о; Kсм = 1,4, крепость породы f = 7, 10, 13). Результаты моделирования приведены в таблицах 3.5 и 3.6. Глубина внедрения изменяется в пределах 0,3–1,0 м, что соответствует реальным значениям при погрузке различных пород.

Рис. 3.19. Алгоритм расчёта вместимости ковша Vк.max или Vк.max1 и объёма, оставшегося в ковше после очередного черпания Vк.з

(начало; окончание см. на с. 84)

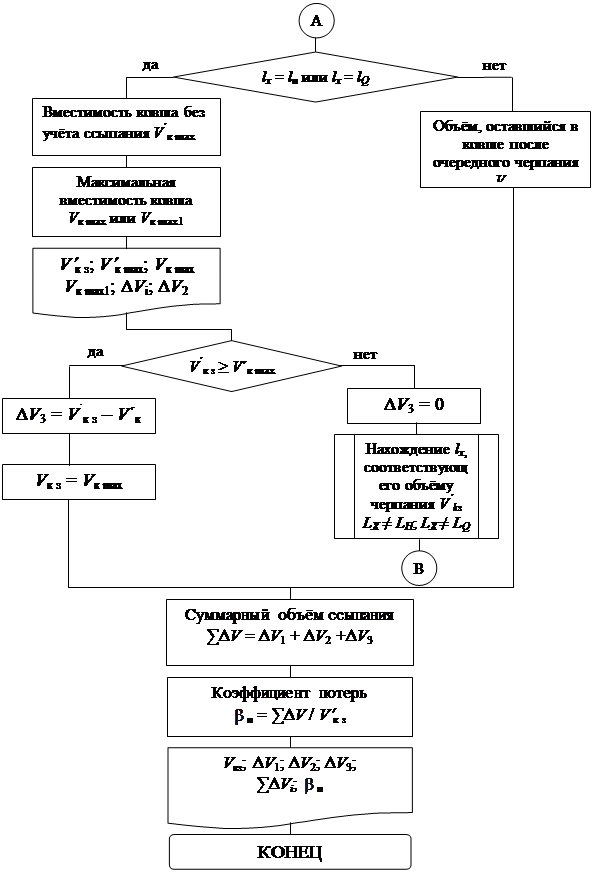
Рис. 3.19. Окончание (начало см. на с. 86)

Таблица 3.5

Максимальная вместимость ковша

 Скачать реферат