Моделирование рабочих процессов погрузочно-транспортных модулей с учетом случайного характера внешних воздействий

.

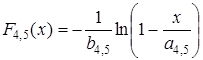Таким образом, получено математическое описание гранулометриче-ского состава штабелей в широком диапазоне изменения среднего размера куска (0,25…0,75) dmax. Это позволяет исследовать влияние состава штабе-ля по крупности на показатели работы погрузочно-транспортных модулей.

2.3 Моделирование гранулометрического соста

ва в малом выделенном объёме

Общие методические подходы. Известные математические модели сопротивлений внедрению ковша и зачерпыванию в качестве основного влияющего фактора учитывают средний размер куска dср, методика определения которого не создана. В качестве dср принимается показатель, относящийся в целом ко всему исходному штабелю горной массы, что делает указанные модели детерминированными. При этом в расчётах устанавливается средняя постоянная глубина внедрения, объём черпания и т.д. Экспериментальные и производственные данные свидетельствуют о том, что рассматриваемые показатели являются случайными величинами с высоким коэффициентом вариации. Поэтому достоверная информация о технических показателях погрузочной машины может быть получена только на основе представления процессов как случайных, при этом главным влияющим фактором должен быть размер куска в различных проявлениях.

Общая схема формирования случайного черпания может быть представлена следующим образом:

1) штабель объёмом V имеет определённый гранулометрический состав, описываемый дискретной функцией распределения F*(x), где x=d/dmax; известна также величина dmax;

2) производится внедрение ковша в штабель; пред кромкой ковша (днищем, боковыми стенками) формируется некоторый локальный объём v, гранулометрический состав которого FV(x) отличается от F*(x); причём в каждом внедрении FV(x) различно;

3) по известному случайному гранулометрическому составу FV(x) перед кромкой ковша формируется средний случайный кусок размером

,

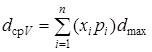где xi – среднее значение случайной величины X по разрядам i Î1, n; pi – вероятность (частость) соответствующих значений xi;

4) в соответствии с размером dcpV реализуется случайная глубина внедрения ковша как минимальная по возможностям механизмов напора и зачерпывания и адекватное ей наполнение ковша, Vк; объём Vк имеет также случайный состав по крупности, который затем передаётся в последующее транспортное средство, например, проходческий перегружатель;

5) к последующему циклу «внедрение – зачерпывание» штабель имеет уже изменённый объём и гранулометрический состав , и затем цикл 2)–5) повторяется с новыми случайными значениями , , FV(x), dcpV, Vк.

Таким образом, для создания имитационной модели формирования потока единичных случайных черпаний необходимо разработать обоснованные процедуры следующих случайных процессов:

а) гранулометрический состав и средний размер куска в малом выделенном объёме v;

б) изменение гранулометрического состава исходного штабеля после очередного черпания.

Гранулометрический состав в малом выделенном объёме. Пусть штабель имеет объём Vо и функцию распределения F(х), где х = d/dmax; х – непрерывная случайная величина, изменяющаяся в пределах (0; 1). Для целей дальнейших исследований интервал (0; 1) разбиваем на N фракций, причём , N – произвольное число. Внутри каждой i-й фракции, i Î (1, N), относительный размер куска принимаем постоянным, равным среднему значению:

.

Функция распределения F(х) на участке (xi-1, xi) принимается постоянной и заменяется ступенчатой с равномерным разбиением по х, причём = F(xсрi) (рис. 2.3). Скачок функции представляет собой вероятность попадания случайной величины в интервал (xi-1, xi) или долю объёма штабеля, занимаемую горной массой со средним размером куска . Обозначив , получим таблицу соответствия xсрi – ai, причём 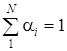. В результате реальный штабель с распределением F(х) заменяется дискретным ai(xсрi).

Для построения имитационной модели формирования гранулометрического состава погружаемого материала в малом выделенном объёме V предлагается генерировать случайным образом число кусков каждого разряда в отдельном опыте. При этом может быть использован известный биноминальный закон распределения [97]:

, (2.1)

где х – дискретная случайная величина, которая может принимать возможные значения 0, 1, 2, …, n; Р(X = m) – вероятность того, что случайная величина X примет значение m; q = 1 – р – вероятность противоположного события; – число сочетаний из n элементов по m.

Рис. 2.3. Замена непрерывного распределения дискретным

Выделенный малый объём V заполняется кусками, представляющими по размерам дискретный ряд xcp1×dmax; xcp.2×dmax; …; xcp.N×dmax. Зная объём V, можно найти максимальное число кусков каждого разряда, которое может разместиться в этом объёме:

.

Таким образом, моделируемая случайная переменная mi в каждом разряде изменяется в пределах 0; 1; 2; …; ni. Для построения дискретного распределения, подчиняющегося биноминальному закону, необходимо определить вероятность единичного события р – попадания куска i-й фракции в объём v. В работе показано, что вероятность р приближенно равна долевому участию по объёму кусков данного разряда i в общем объёме штабеля.

Теперь, по известным ni и i, можно построить биноминальный закон распределения вероятности выпадения числа кусков данного разряда mi в пределах от 0 до ni. На основе этого закона в каждом черпании можно с использованием генератора случайных чисел задавать случайное значение mi – число кусков i-го разряда, попавших в ковш, перед кромкой ковша, лапы, клина и т.д.

Проверка адекватности моделирования реальному гранулометрическому составу штабеля должна проводиться после k опытов (число k может быть установлено на основе распределения Стьюдента для малого объёма выборки). По каждому разряду среднее значение приближается к математическому ожиданию: mxi = ni i.

 Скачать реферат